組合せとグラフの理論(塩田)第8回 (3) 郵便配達員問題
問題設定
郵便配達員問題 連結な重み付きグラフ $G$ において、
全ての辺を 1 回以上通る閉じた歩道で重み最小のものを求めよ。
※ 郵便配達員さんは全ての道を通って配達をして、最後は郵便局へ帰って来なければなりません。
その最短ルートを求める問題です。
オイラーグラフ・半オイラーグラフの場合
Prop.8 $G$ がオイラーグラフであれば、オイラーサーキットが郵便配達員問題の解である。
証明 定義より。(証明終)
Prop.9 $G$ がオイラーグラフでない半オイラーグラフであれば、
以下のアルゴリズムにより郵便配達員問題の解が求まる。
- 奇数次数の 2 頂点を $u$, $v$ とする。
- Alg.5 を用いて最短の $u$-$v$ 道 $P$ を求める。
- $P$ 上の辺を二重化したグラフを $G'$ とする。
- $G'$ のオイラーサーキットを出力する。
Ex.10 次のグラフで郵便配達員問題を解きましょう。
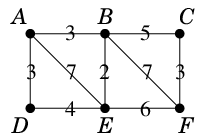
奇数次数の頂点は $A$, $F$ の 2 個なので、
最短の $A$-$F$ 道を求めると
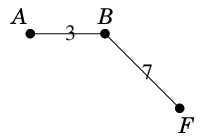
となります。
この辺を二重化すると図のように全ての頂点の次数が偶数になり、
そのオイラーサーキットが解になります。

奇数次数の頂点が 4 個の場合
では奇数次数の頂点が 4 個のときはどうでしょうか。
Ex.11 次のグラフで郵便配達員問題を解きましょう。
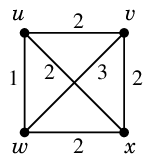
やはり何本かの辺を二重化してオイラーグラフにします。
今度は奇数次数の頂点が 4 個ですので、
2 本以上の辺を二重化する必要があります。
 |
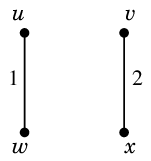 |
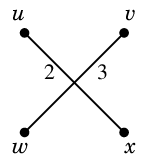 |
(1) $uv$ と $wx$ を二重化
$\Rightarrow$ 重みは 4 増える |
(2) $uw$ と $vx$ を二重化
$\Rightarrow$ 重みは 3 増える |
(3) $ux$ と $vw$ を二重化
$\Rightarrow$ 重みは 5 増える |
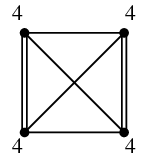
(2) の場合が重みが最小になるので、
$uw$ と $vx$ を二重化したグラフでオイラーサーキットを求めます。
もっと一般の場合
これを一般化すると
Prop.12 連結な重み付きグラフ $G$ において、
奇数次数の頂点が $u$, $v$, $w$, $x$ の 4 個であれば、
以下のアルゴリズムにより郵便配達員問題の解が求まる。
- Alg.5 を用いて
- 最短の $u$-$v$ 道と、最短の $w$-$x$ 道
- 最短の $u$-$w$ 道と、最短の $v$-$x$ 道
- 最短の $u$-$x$ 道と、最短の $v$-$w$ 道
を求める。
- 1°の 3 通りのうち、距離の合計が最小の場合の、最短路上の辺を二重化したグラフを $G'$ とする。
- $G'$ のオイラーサーキットを出力する。
Rem.13 奇数次数の頂点が多数あるときは、
Prop.12 1°のような組み合わせの場合の数が膨大になるので、
後日勉強する「マッチング」のアルゴリズムを応用することになります。







