組合せとグラフの理論(塩田)第6回 (3) 幅優先探索
アルゴリズム
教科書では p.79 で簡単に書いてありますが、大事なアルゴリズムですので時間を掛けてやりましょう。 「根 ( root )」と呼ばれる頂点を与えて、その根から木を伸ばしてゆきます。
Algorithm 11(幅優先探索、BFS = Breadth-First-Search )
- 入力:連結なグラフ $G$ と、その頂点 $v$
- 出力:$v$ を根とする $G$ の幅優先探索木 $T$
- $v$ を要素とするキュー $Q=\{\,v\,\}$ を作り、 $T$ の初期値は $v$ 一点からなる木とする。
- $Q$ の先頭から $x$ を取り出し、$x$ の未探索な隣接点のすべてを、番号の小さい順に
$y_1$, $y_2$, $\cdots$, $y_s$ とする。 - $Q$ の最後尾に $y_1$, $y_2$, $\cdots$, $y_s$ をこの順で追加し、 $T$ には辺 $xy_1$, $xy_2$, $\cdots$, $xy_s$ をすべて追加する。
- $Q$ が空(くう)リストになれば $T$ を出力して終了。そうでなければ 2°へ戻れ。
例題
Ex.12 まずは二分木の場合に、チョー丁寧に動作を確認してみましょう。
次の図で $v=0$ を根として幅優先探索を実行します。 最初は、キューが $Q=\{\,0\,\}$, 赤い部分が $T$ です。
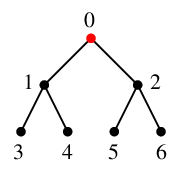
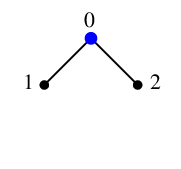
$x=0$ を $Q$ から取り出し、これを探索点(青い頂点)とします。 一旦 $Q$ は空になります。
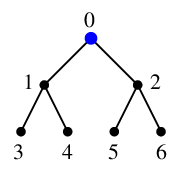
$x=0$ の隣接点 $1$, $2$ はどちらも未探索ですから $y_1=1$, $y_2=2$ になり、
$T$ には辺 $01$ と $02$ を追加、$Q=\{\,1,2\,\}$ になります。
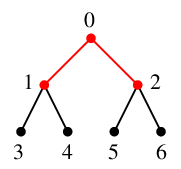
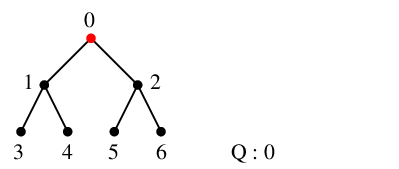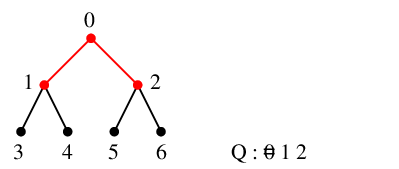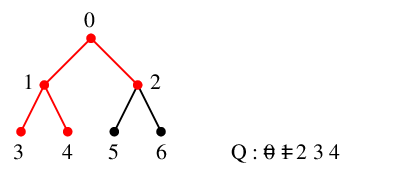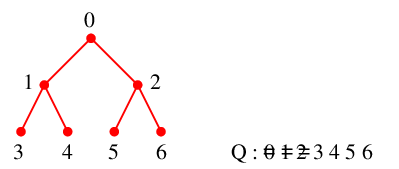
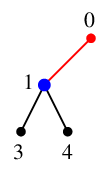
$x=1$ を $Q$ の先頭から取り出し、これを探索点とします。 $Q=\{\,2\,\}$ になります。
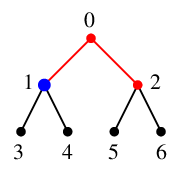
$x=1$ の隣接点 $0$, $3$, $4$ のうち未探索なのは $y_1=3$, $y_2=4$ の 2 つで、
$T$ には辺 $13$ と $14$ を追加、$Q=\{\,2,3,4\,\}$ になります。
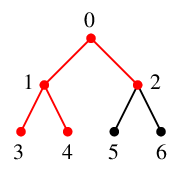
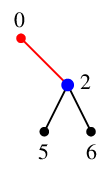
$x=2$ を $Q$ の先頭から取り出し、これを探索点とします。 $Q=\{\,3,4\,\}$ になります。
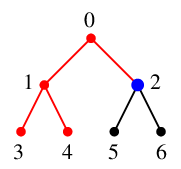
$x=2$ の隣接点 $0$, $5$, $6$ のうち未探索なのは $y_1=5$, $y_2=6$ の 2 つで、
$T$ には辺 $25$ と $26$ を追加、$Q=\{\,3,4,5,6\,\}$ になります。
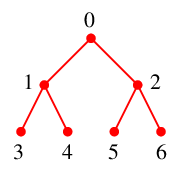
未探索点が無くなりましたので人間がやるときはここでおしまいです。
(アルゴリズム的にはこのあと、$3$, $4$, $5$, $6$ を $Q$ から取り出して $Q$ が空になって終了します。)
次の図で $v=0$ を根として幅優先探索を実行します。 最初は、キューが $Q=\{\,0\,\}$, 赤い部分が $T$ です。







Rem.13(ここ大事!)自分が探索点 $x$(青い頂点)に立っていて、
$x$ の隣接点までしか見ることができない、というイマジネーションを働かせてください。
Ex.12 ではそれぞれの場面で
しか見えていなくて、探索済みの赤い頂点以外の、黒い頂点たち全てへ幅広く木を伸ばす、
と考えます。
※ 慣れてくれば、キューを横に書くだけで作業できるようになります。
Ex.12 ではそれぞれの場面で
 |
 |
 |
||
| $x=0$ のとき | $x=1$ のとき | $x=2$ のとき |
※ 慣れてくれば、キューを横に書くだけで作業できるようになります。

Ex.14 もうひとつ、木ではないグラフで、もっとラフにやってみます。やはり $v=0$ を根とします。
根 $v=0$ から探索を開始します。
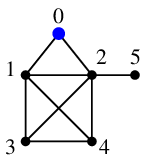
探索点 $0$ から未探索点 $1$, $2$ が見えますので、
$0$ から $1$, $2$ へ辺を伸ばします。
探索点は、キュー $Q=\{\, 1,2\,\}$ の先頭要素 $1$ に移します。
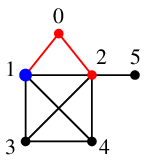
探索点 $1$ から未探索点 $3$, $4$ が見えますので、
$1$ から $3$, $4$ へ辺を伸ばします。
探索点は、キュー $Q=\{\, 2, 3, 4\,\}$ の先頭要素 $2$ に移します。
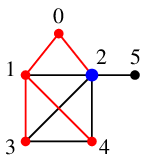
探索点 $2$ から未探索点 $5$ が見えますので、$x=2$ から $5$ へ辺を伸ばして終了です。
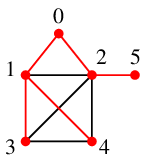
根 $v=0$ から探索を開始します。



