組合せとグラフの理論(塩田)第4回 (4) 辺連結度・連結度
辺連結度
連結なグラフ $G=(V,E)$ について、どの位強く連結であるか、を数値として表現しましょう。
Def.10
- $e \in E$ に対し、$G-e$ が非連結になるとき $e$ を「橋」と呼ぶ。
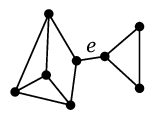 |
→ |
 |
| | $G-e$ |
- 辺の部分集合 $F \subset E$ に対し、$G-F$ が非連結になるとき $F$ を「非連結化集合」と呼ぶ。
- 極小な非連結化集合を「カットセット」と呼ぶ。
「$F$ が
極小な 非連結化集合である」とは、$F$ 自身は非連結化集合であるが、
$F$ のどんな真部分集合も非連結化集合にならない、ということです。
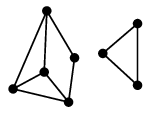
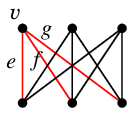
Ex.11 次のグラフ
において、
- $F=\{\,e,f,g\,\}$ は非連結化集合です:
$G-F$
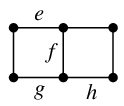
しかし、$F$ はカットセットではありません。なぜなら、$F$ の真部分集合 $F'=\{\,e,g\,\}$ に対しても $G-F'$ が非連結になるからです:
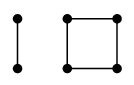
$G-F'$
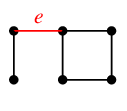
- $F'$ はカットセットです。
$e$ または $g$ を復活させると連結に戻るからです。
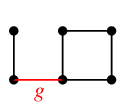
- $F''=\{\,e,f,h\,\}$ もカットセットです:
$G-F''$
※ カットセットの辺数は一定とは限りません。
Def.12 $G$ の辺連結度とは
$\lambda(G)=$ ( カットセットの辺数の最小値 )
( $\lambda$ はギリシャ文字のラムダ )
例えばコンピュータネットワークを表すグラフにおいては、
カットセットに属する回線が全て切れてしまうと通信ができなくなります。
従って、$\lambda(G)$
が大きいほどネットワークは安全、ということになります。
Rem.13
- 橋 $e$ は1本だけでカットセットになる。
( $G-e$ は非連結、$G$ は連結ゆえ。)
- 橋が存在すること $\Leftrightarrow$ $\lambda(G)=1$.
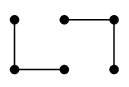
- Ex.11 では $\lambda(G)=2$.
( 橋は無いので $\lambda(G) \geqq 2$ であり、$F''$ は辺数 2 のカットセットゆえ。)
... $F''$ ではなく $F'$ が辺数 2 のカットセットでした ( 5月15日訂正 )
連結度
次は頂点に関する連結度を考えます。
Def.14
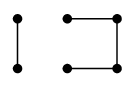
- $v \in V$ に対し、$G-v$ が非連結になるとき $v$ を「カット点」と呼ぶ。
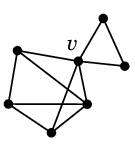 |
→ |
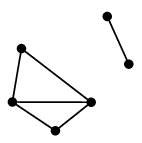 |
| | $G-v$ |
- 頂点の部分集合 $W \subset V$ に対し、$G-W$ が非連結になるとき $W$ を「分離集合」と呼ぶ。
Ex.15 次のグラフ
において、
$W=\{\,v,x\,\}$ や $W'=\{\,v,y\,\}$ は分離集合の例です:
 |
|
 |
| $G-W$ | | $G-W'$ |
Def.16 $G$ の連結度とは
$\kappa(G)=$ ( 分離集合の頂点数の最小値 )
( $\kappa$ はギリシャ文字のカッパー )
コンピュータネットワークを表すグラフにおいては、
分離集合に属するサーバが全てダウンしてしまうと通信ができなくなります。
辺連結度と同様に、$\kappa(G)$
が大きいほどネットワークは安全、ということになります。
Rem.17
- カット点 $v$ は1個だけで分離集合になる。
( $G-v$ は非連結、$G$ は連結ゆえ。)
- カット点が存在すること $\Leftrightarrow$ $\kappa(G)=1$.
- Ex.15 では $\kappa(G)=2$.
( カット点は無いので $\kappa(G) \geqq 2$ であり、$W$ は頂点数 2 の分離集合ゆえ。)
Th.18
$\kappa(G) \leqq \lambda(G) \leqq$ ( $G$ の頂点の次数の最小値 )
証明 次数が最小の頂点を $v$、$v$ の接続辺の全てを $W$ とすると、$G-W$ では $v$ が孤立点となって非連結になりますから
$\lambda(G) \leqq v$ の次数
であることがわかります。
 |
→ |
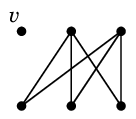 |
| $W=\{\,e,f,g\,\}$ | | $G-W$ |
あとは [7] Bondy-Murty P.37 を見てください。( 教科書末の文献表参照 )














