戻る / 次へ

(1)　完全グラフ $K_n$

　オーダー $n$ で、全ての頂点が互いに隣接している単純無向グラフのこと。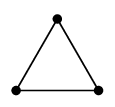

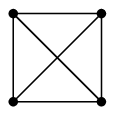$K_3$		$K_4$		$K_5$

復習しておきますが、オーダーは頂点数、サイズは辺数です ( 時間節約のためにアチャラ語で書いています )。

(2)　空グラフ $N_n$

　辺を持たない、オーダー $n$ のグラフのこと。「くうグラフ」と読みます。辺集合が空集合、という意味です。

$N_3$		$N_4$

(3)　正則グラフ

　全ての頂点の次数が等しいグラフのこと。（これは固有名詞ではありません。） その次数が $r$ のとき、$r$-正則グラフと呼んだり、$r$-正則である、と言ったりします。 例えば、

• $K_n$ は $(n-1)$-正則グラフ
• $N_n$ は $0$-正則グラフ

です。

　正則グラフの中でも美しくて有名なのが

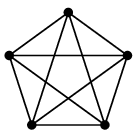
(4)　ペテルセングラフ（ピーターセングラフ）

　オーダー 10, サイズ 15, 3-正則な次のグラフのことです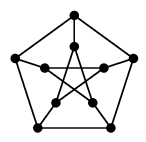： シンプルでありながら、平面的でない、ハミルトングラフではない、など、いろいろな概念の例としてよく使われます。

　五角形の中に星を描いて内と外をつなげばよいので、自分でも描けるようになりましょう。 　→　 　→　

命題をひとつ

証明　前回の握手補題より $2$ $\times$ サイズ $=$ 次数の和 $=$ $r \times n$ ゆえ。(証明終)

　例えばペテルセングラフでは $n=10$, $r=3$ で $rn/2=15=$ サイズ、になります。
　次も正則グラフの例です：

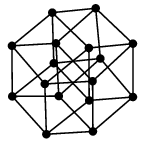
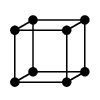
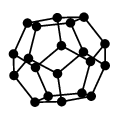
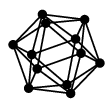
(5)　プラトングラフ

　正多面体の頂点と辺から作ったグラフをプラトングラフと呼びます。5種類あります。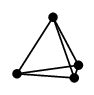

正四面体グラフ		立方体グラフ		正八面体グラフ

正十二面体グラフ		正二十面体グラフ

これらは辺の交差無く描くこともできます：

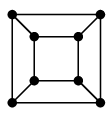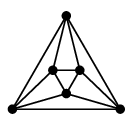正四面体グラフ		立方体グラフ		正八面体グラフ

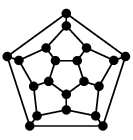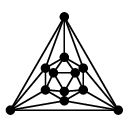正十二面体グラフ		正二十面体グラフ

(6)　二部グラフ

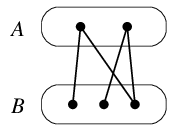
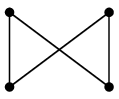
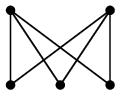
　頂点集合 $V$ が交わりの無い２つの部分集合 $A$, $B$ に分かれ ( $V=A \cup B$,   $A \cap B = \emptyset$ )、 $A$ に属する頂点と $B$ に属する頂点の間にしか辺が無いグラフを二部グラフと呼びます。 $A$ の頂点同士、$B$ の頂点同士は隣接しない、と言っても同じです。

(7)　完全二部グラフ $K_{m,n}$

　上の状況で、特に

• $|\,A\,|=m$, $|\,B\,|=n$ で、
• $A$ の頂点と $B$ の頂点は必ず隣接する

ものを完全二部グラフと呼び、$K_{m,n}$ と表します。

$K_{2,2}$		$K_{2,3}$

(8)　星グラフ

　$K_{1,n}$ のことですが、頂点の配置によって星の形に見えるので星グラフと呼びます。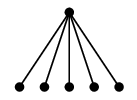

		$\cong$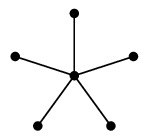
$K_{1,5}$				こう描けば星の形

ネットワーク論で「スター型」というやつです。

(9)　閉路 $C_n$

　$n$ 頂点の、輪の形のグラフです。$n$ 角形の頂点と辺から作ったグラフ、と言っても同じです。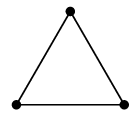

$C_3$		$C_4$

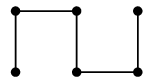
(10)　道グラフ $P_n$

　$n$ 頂点の、一直線の形のグラフです。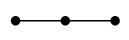

$P_3$		$P_4$

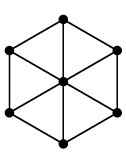
(11)　車輪グラフ $W_n$

　$n$ 頂点の、文字通り車輪の形のグラフです。 真ん中にも点があるので　$W_n$ は $n-1$ 角形の車輪です。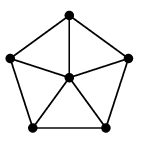

$W_6$		$W_7$

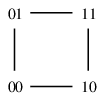
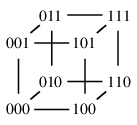
(12)　$k$ 次元立方体グラフ $Q_k$

　$k$ 次元立方体の頂点と辺から作ったグラフです。 言葉を変えるとこういう定義もできます：

• 長さ $k$ のビット列を頂点とする。
• 1 ビットだけ違うビット列同士を辺で結ぶ。

$k=2,\,3$ の場合を描いてみると、

$Q_2 \cong C_4$		$Q_3 \cong$ 立方体グラフ

それぞれ $xy$-平面の単位正方形、$xyz$-空間の単位立方体になっていますね。
※　$Q_k$ の中での距離は、符号理論で用いる「ハミング距離」と同じもので、信号の誤り訂正能力に関わる重要な概念です。

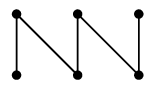
形は変えてもいい

　以上、「何々の形をした」という書き方をしましたが、同型なグラフは「同じもの」として同じ名前で呼びますので、 頂点の配置は自由に動かして構いません。ここ大事 !
　たとえば直線の形はしていませんが、次のグラフたちも $P_6$ です：   

戻る / 次へ