組合せとグラフの理論(塩田) 2020年度 第14回
今日のテーマ
-
マッチングという言葉は、例えば就職活動ではマッチングセミナーを連想します。
これは学生の希望職種と企業側の求める人材が合致することを目的としていますが、
このように「相性のいいペアを作ってあげたい」という状況を抽象的に表現したのがグラフのマッチングです。
$\newcommand{\ol}[1]{\overline{#1}}$
$\newcommand{\card}[1]{\left|\,#1\,\right|}$
1. まずは定義から
問 1 10人の刑事を2人ずつのペアにして捜査を行いたい。
ただし、気の合わない者をペアにして支障をきたすといけないので、
気の合う者同士のペアを作ることにする。
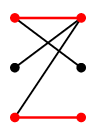
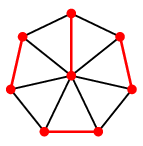
「気の合う関係」が次のグラフで表されるとき、どのようなペアを作ればよいか。

解
図の赤い辺をペアとすれば 10 人全員が捜査に携われます。
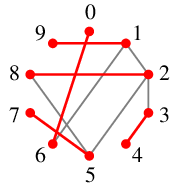
「俺はこいつとしか気が合わん」という刑事さんがたくさんいましたが ( $0$, $4$, $7$, $9$ )、
なんとかペアが作れて良かったですね。
このように辺の中からいくつかを選んで頂点のペアを作ったものをマッチングと言います。
グラフ理論用語で定義を書くと次のようになります。
Def.2 単純無向グラフ $G$ の $1$-正則な部分グラフをマッチングと呼ぶ。
他にもいくつか例を見てみましょう。
気持ちとしてはたくさんペアを作れる方が嬉しいので、次の定義をします。
Def.4 辺の本数が最大となるマッチングを「最大マッチング」と呼ぶ。
さらに「全ての頂点を含むマッチングが存在するか」
ということを考えるのですが、二部グラフか否かで様相が違いますので、
まずは二部グラフを扱いましょう。
2. 二部グラフの完全マッチング
二部グラフのマッチングは「結婚問題」という観点で述べられます。
結婚問題 適齢期の女性 $m$ 人、男性 $n$ 人のグループがあるとする ( $m \leqq n$ )。
全ての女性がこのグループ内の知り合いの男性と結婚することができるか。
Ex.5 知り合い関係が次の表で表されているとします。
| 女性 | 知り合いの男性 |
| $a$ | $A$, $D$ |
| $b$ | $A$, $C$ |
| $c$ | $B$, $D$, $E$ |
| $d$ | $C$, $E$ |
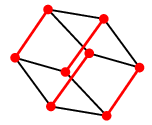
この関係をグラフで表現すると

このグラフで次のようなマッチングを取れば全ての女性が知り合いの男性と結婚できます。

※ 男性が余っていますが、「そこは気にしていない」ことを気に留めておいてください。
Def.6 二部グラフ $G=G(V_1, V_2)$ において、
$V_1$ に属する頂点をすべて含むマッチングを
「$V_1$ から $V_2$ への完全マッチング」と呼ぶ。
結婚問題は $V_1=\{$ 女性 $\}$, $V_2=\{$ 男性 $\}$ としたときに
$V_1$ から $V_2$ への完全マッチングが存在するか、という問題です。
繰り返しますが、二部グラフの完全マッチングでは $V_2$ の頂点は余ってもいいことにします。
Th.7(ホールの結婚定理) $V_1$ の部分集合 $A$ に対して
$\varphi(A)=\{\,A$ に属する頂点の隣接点たち $\}$
を $A$ の近傍と言う( $\varphi(A)$ は $V_2$ の部分集合である )。
このとき、
$V_1$ から $V_2$ への完全マッチングが存在すること
$\Leftrightarrow$
任意の $A \subseteq V_1$ に対して
$\card{\varphi(A)} \geqq \card{A}$ が成り立つこと $\cdots$ $(\ast)$
証明 $\Rightarrow$) は当然成り立たねばなりません。
$V_1$ から $V_2$ への完全マッチングにおいては、
$A$ の頂点の隣接点はすべて異なるのですから $\card{\varphi(A)} \geqq \card{A}$ となります。
$\Leftarrow$) は次のアルゴリズムを実行します。
Algorithm 8
- 次のようにネットワーク $N$ を作る。
- $G$ の各辺を、$V_1$ から $V_2$ の方向へ向かう重み 1 の弧に置き換える
- 入口 $v$ と出口 $w$ を付加する
- $v$ から $V_1$ の全ての頂点へ、$V_2$ の全ての頂点から $w$ へ重み 1 の弧を作る
 $\longrightarrow$
$N$ :
$\longrightarrow$
$N$ : 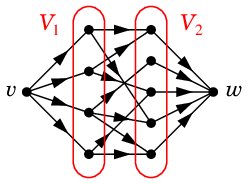
- $N$ の最大フロー $\Phi$ を求める。
$\Phi$ :

- $\Phi$ から $v$, $w$ を除去し無向化したグラフ $M$ を出力する。

この $M$ が $V_1$ から $V_2$ への完全マッチングになることは次の補題で示します。
Lemma 9 Alg.8 のネットワーク $N$ の最小カットの容量は $\card{V_1}$ に等しい。
従って最大フロー・最小カット定理により
Alg.8 3° の $M$ は $V_1$ から $V_2$ への完全マッチングになる。
証明 $B=(S, \ol{S})$ を任意のカットとすると、
$S$, $\ol{S}$ は次のように分割できます:
$S=\{\,v\,\} \cup X \cup Y$,
$\ol{S}=X' \cup Y' \cup \{\,w\,\} $.
ただし
$X = S \cap V_1$,
$Y = S \cap V_2$,
$X' = \ol{S} \cap V_1$,
$Y' = \ol{S} \cap V_2$.
記号で書くより、次のように図示した方が分かり易いでしょう
( 青い部分が $S$, 緑が $\ol{S}$, 赤い弧たちが $B$ です )。

すると $B$ に属する弧は次の 3 種類になります:
- $v$ から $X'$ の頂点に至るもの
- $X$ の頂点から $Y'$ の頂点に至るもの
- $Y$ の頂点から $w$ に至るもの
$N$ の作り方から (i) の弧は $\card{X'}$ 本、(iii) の弧は $\card{Y}$ 本です。
また、$\varphi(X) \cap Y' = \varphi(X) - Y$ の各頂点へは $X$ からそれぞれ 1 本以上の弧がありますので、
(ii) の弧は最小でも $\card{\varphi(X)-Y}$ 本以上あります。
以上から
\begin{align}
B \mbox{ の容量 } &\geqq \card{X'} + \card{Y} + \card{\varphi(X) - Y} \\
&\geqq \card{X'} + \card{Y} + \card{\varphi(X)} - \card{Y} \\
&\geqq \card{X'} + \card{X} = \card{V_1} \\
\end{align}
これで、任意のカットの容量が $\card{V_1}$ 以上であることが言えました。
特に $S=\{\,v\,\}$, $\ol{S}=V_1 \cup V_2 \cup \{\,w\,\}$ の場合、
$B=(S,\ol{S})$ は $v$ から $V_1$ の頂点へ至る弧の集合ですからその容量は $\card{V_1}$ であり、
これが最小カットになります。(証明終)
たとえ完全マッチングが存在しないときでも、
$N$ の作り方より次が成り立ちます。
Th.10 $(\ast)$ の成立・不成立に関わらず、
Alg.8 は二部グラフ $G=G(V_1, V_2)$ の最大マッチングを与える。
Rem.11 二部グラフの最大マッチングを求めるアルゴリズムとしては、
もうひとつ、「ハンガリー・アルゴリズム」が有名です。
3. 一般のグラフの完全マッチング
今度は二部グラフに限らず、一般のグラフのマッチングを考えます。
完全マッチングの定義が二部グラフとは異なりますので注意してください。
ここ大事!
Def.12 一般のグラフにおいては、全ての頂点を含むマッチングを「完全マッチング」と呼ぶ。
ペテルセングラフは次の定理の代表例です。
Th.14(ペテルセンの定理) 橋を持たない $3$-正則グラフは完全マッチングを持つ。
(証明略)
Rem.15
- 完全マッチングは自動的に最大マッチングでもある。
- 最大マッチングは常に存在するが、完全マッチングは存在するとは限らない。
- 例えば頂点数が奇数なら完全マッチングは存在し得ない。
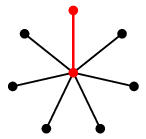
例えば星グラフ $K_{1,n}$ ( $n \geqq 2$ ) の最大マッチングは辺 1 本だけです。
与えられたグラフが完全マッチングを持つかどうかは、
最大マッチングに全ての頂点が含まれるか否か、で判定します。
4. 一般のグラフの最大マッチングアルゴリズム
最大フローアルゴリズムと同様に「増加道」というものが登場します。
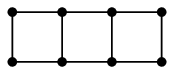
Def.16 $M$ を $G$ のマッチングとする。( $M$ はゼロマッチングでもよい。)
このとき、
- $G$ 内の道であって
- $M$ の辺を交互に含み
- 始点と終点がどちらも $M$ に属さないもの
を $M$-増加道と呼ぶ。
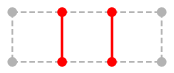
Prop.18 $P$ が $M$-増加道であれば、辺集合として
$M'=P \oplus M = P$ XOR $M$
とおくことにより、$M'$ は $M$ が辺が 1 本多いマッチングとなる。
Ex.17 では
$M \oplus P$ : 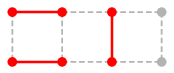 ,
$M \oplus Q$ :
,
$M \oplus Q$ : 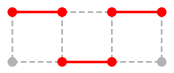
いずれも $M$ より 1 本辺が増えています。
Th.19 $M$ が最大マッチングであること $\Leftrightarrow$ $M$-増加道が存在しないこと。
(証明略)
※ 従って、最大マッチングアルゴリズムには
$M$-増加道を検索するアルゴリズムが必要ですが、
その決定版は Edwards の Blossom アルゴリズム ( 1965年 ) です。
塩田のグラフ描画ツールでも Blossom アルゴリズムを用いて実装していますが、恐ろしく複雑です。
Rem.20
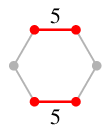
重み付きグラフでは、重みの合計が最大になるようなマッチングを考えることができます。
- たとえば最初の刑事さんの例で、「相性の良さ」を重みとすれば、
相性の良さの合計が最大になるような組み合わせを考えることになります。
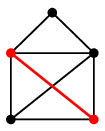
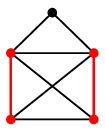
- 重み最大マッチングは、辺数最大のマッチングとは異なることがあります。
 $\Rightarrow$
重み最大マッチングは
$\Rightarrow$
重み最大マッチングは
- 郵便配達員問題は、奇数次数の頂点がたくさんあるときは、
重み最大マッチングアルゴリズムを応用して解きます。
本講義のまとめ
この講義では、
- もののつながりを「グラフ」として表現し
- もののつながり方に関する問題を「グラフ問題」として抽象的に読み替え
- 「グラフの定理」や「グラフ・アルゴリズム」で解く
ということを学びました。
見た目が違っても抽象度を上げれば同じもの、ということが世の中にはたくさんあって、
それを見破ることが問題解決の大きな助けになることも少なくありません。
この講義を通じてそういう力が少しでも身に付けてもらえたなら幸いです。
大変な状況の中、半期の間ご苦労さまでした。あとひとつ、学期末レポートをクリアしてください。
学期末レポート
- 今日は宿題はありませんが、対面試験ができない代わりに学期末レポートを課します。
- 締め切りは来週 8月7日(金) 12:00 とします。
- ここから download(全4ページ5問)
- 宿題と同様、pdf, 画像ファイル等の形で、
shiota@is.kochi-u.ac.jp 宛に送信してください(@は小文字)。
- 上手く送信できない人は相談してください。
戻る















 ,
$Q$ :
,
$Q$ : 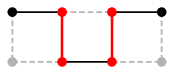
 ,
$M \oplus Q$ :
,
$M \oplus Q$ : 
 $\Rightarrow$
重み最大マッチングは
$\Rightarrow$
重み最大マッチングは
