組合せとグラフの理論（塩田）　2020年度第11回

今日のテーマ

点彩色

　第１回に、地図を塗り分ける「四色問題」のお話をしました。前回は双対グラフを勉強して、「面」を塗り分けることは、双対グラフの「頂点」を塗り分けることに読み替えると処理しやすい、という話をしました。
　今日はその、頂点の塗り分け ― 専門用語で「点彩色」 ― の勉強をします。

1.　点彩色の定義と、基本的命題

　まずは定義から。

Def.1　

$G$ をループを持たない無向グラフとする。

$G$ の頂点に色を割り当て、隣接する頂点同士は別の色になるようにすることを「

$G$ の点彩色」という。

Ex.2　次のグラフに点彩色を施してみましょう。実際に色を塗るのは大変なので、色の番号を振って表します。

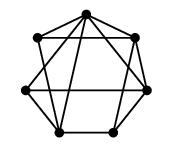
全ての頂点に異なる色を使えば当然点彩色になります。

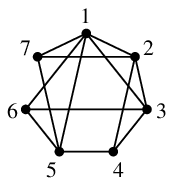
もっと少ない色で点彩色してみましょう。隣接していなければ同じ色を塗ってもよいので

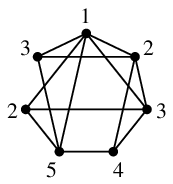とか

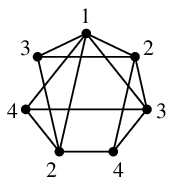
でもOKです。

　色をたくさん使えば色は塗り易くなります。しかし色が多いほどコストは増えます（インクをたくさん買わなければならない、とか）。そこで、なるべく使う色を少なくしよう、というのが次の定義です。

Def.3　

$G$ が $k$ 色で点彩色できるとき「 $G$ は $k$ -彩色可能である」という。
$G$ が点彩色できる最少の色数を「 $G$ の彩色数」と呼び、 $\chi(G)$ と表す。

彩色数の示し方　

$\chi(G)=k$ であることを示すには

$G$ を点彩色するには $k$ 色以上必要であることを示し、かつ
$G$ が本当に $k$ 色で点彩色できることを示す。

　1° は、

$G$ が

$k-1$ 色以下では点彩色できないことを示すことと同じです。

※　必要最小限と言わないといけないので 1° を忘れてはいけません。 こことても大事！！ （毎年口を酸っぱくして教えているのですが ... ）

Ex.4　

$\chi(C_5)=3$ .

2 色で点彩色しようとすると互い違いに色を使うしかなく、5 つ目の頂点にはどちらの色も使えなくなります。
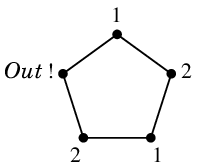
次のように塗れば 3 色で点彩色できます。

　基本的な性質を命題としてまとめていきましょう。

Prop.5　

$\chi(G)=1$ であることと、 $G$ が空グラフであることは同値である。
$\chi(G)=2$ であることと、 $G$ が空でない二部グラフであることは同値である。
$T$ が 2 頂点以上の木であれば $\chi(T)=2$ である。
$\chi(K_n) = n$ .
$n \geqq 3$ に対して $\dps{\chi(C_n)=\left\{ \begin{array}{ll} 2 & n \mbox{ が偶数のとき} \\ 3 & n \mbox{ が奇数のとき.} \\ \end{array} \right.}$

証明　

$G$ が空グラフであれば隣接関係が全くないので $\chi(G)=1$ です。辺が 1 本でもあればその両端に違う色を使う必要があるので $\chi(G) \geqq 2$ になります。
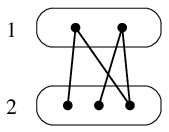
$G$ は空でないので $\chi(G) \geqq 2$ であり、次のように 2 色で点彩色できます。
木は二部グラフゆえ。
完全グラフは全ての頂点が互いに隣接していますので、全ての頂点に違う色を使う必要があります。
Ex.4 のように、 $n$ が偶数なら互い違いに塗ればよく、 $n$ が奇数なら 3 色目が必要になります。

(証明終)

Prop.6　

$H$ をグラフ

$G$ の部分グラフとすると

$\chi(H)$ _□

$\chi(G)$ .
... □ には

$\leqq$ と

$\geqq$ のどちらが入るでしょうか。

答えは自分で考えてから

Prop.6　

$H$ をグラフ

$G$ の部分グラフとすると

$\chi(H) \leqq \chi(G)$ .

証明　

$G$ を

$\chi(G)$ 個の色で点彩色しておけば、そこからいくつかの頂点と辺を除去した

$H$ の点彩色にもなっています。点彩色可能な色数の最小値が

$\chi(H)$ なので

$\chi(H) \leqq \chi(G)$ です。(証明終)

　平面性の問題では部分グラフの方が描き易かったのと同様、部分グラフの方が束縛条件が少ないので色が塗り易い、ということです。

Prop.7　

$G$ が部分グラフとして

$K_n$ を含んでいれば

$\chi(G) \geqq n$ .

Ex.8　一筆書きでよく使うこのグラフは

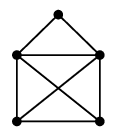
$K_4$ を部分グラフとして含んでいますので彩色数は 4 以上で ( 1° )、実際に次のように 4 色で点彩色できます ( 2° )。

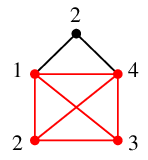
　この例のように Prop.7 は 彩色数の示し方 の 1°　に役立つのですが、残念なことに逆が成り立ちません。

Rem.9　

$\chi(G)=n$ であっても

$G$ が

$K_n$ を含むとは言えない。 ここもとても大事！！

　次の節では Rem.9 のような

$G$ を作って見せます。

2.　 $K_n$ を含まないのに彩色数が $n$ であるグラフの作り方

Ex.4 再掲　

$C_5$ は

$K_3$ を含まないが

$\chi(C_5)=3$ .

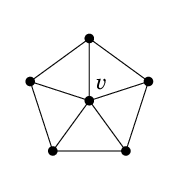
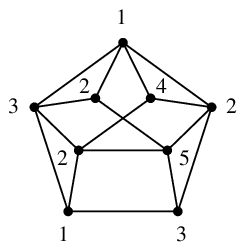
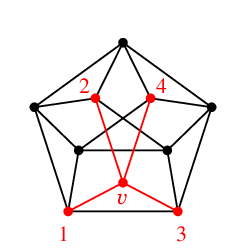
Ex.10　

$W_6$ は

$K_4$ を含まないが

$\chi(W_6)=4$ .

証明　

$W_6$ は、

$C_5$ に頂点

$v$ をひとつ追加して、

$v$ とその他の頂点全てを隣接させたグラフです。

$C_5$ の部分を点彩色するのに 3 色必要で、さらに

$v$ にはその 3 色と違う 4 色目が必要となりますので

$\chi(W_6)=4$ になります。

→

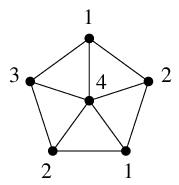
$W_6$ が

$K_4$ を含まないことは背理法で示します。もし

$W_6$ が

$K_4$ を含んでいると仮定すると、

$W_6$ から 1 頂点を除去したグラフには、

$K_4$ から 1 頂点を除去したグラフ

$K_3$ が含まれなければなりません。しかし、

$W_6 - v$ は

$C_5$ ですから

$K_3$ は含みません。(証明終)

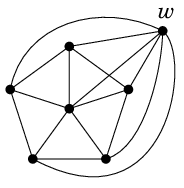
Ex.11　

$K_5$ を含まないが

$\chi(G)=5$ であるグラフは次のように構成できる。　

$W_6$ に頂点 $w$ をひとつ追加する。
$w$ とその他の頂点全てを隣接させる。

　証明は Ex.10 と全く同様です。

$W_6$ の部分の点彩色に 4 色必要で

$w$ には 5 色目が必要。

$G-w$ は

$W_6$ ゆえ

$G$ が

$K_5$ を含むと仮定すると矛盾が生じます。

→

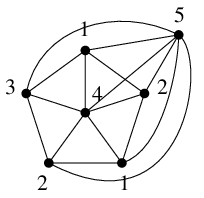
　Ex.11 の操作を続けてゆけば、全ての

$n \geqq 6$ についても「

$K_n$ を含まないのに彩色数が

$n$ であるグラフ」を構成できます。

3.　スケジュール調整問題と彩色問題の関係

問　次の表のように 10 人のメンバー

$A,B,\cdots,J$ が6つの委員会

$u,v,\cdots,z$ に所属しているとする。各委員にとって会議が重ならないように、最小のコマ数で6つの委員会の時間帯を設定せよ。

委員会	構成員
$u$	$A$	$B$	$C$	$D$	$E$
$v$			$C$	$D$	$E$	$F$	$G$
$w$						$F$	$G$	$H$	$I$
$x$								$H$	$I$	$J$
$y$	$A$	$B$								$J$
$z$	$A$	$B$	$C$		$E$		$G$	$H$	$I$	$J$

解　この問題を点彩色を使って解きましょう。グラフを描く訳ですが、まず

頂点は委員会
色は時間帯

とします。では辺は何かと言うと、「隣接する委員会には違う時間帯を割り振る」という条件を付けることになるので

ひとりでも構成員が重なる委員会同士は隣接させる

ことにします。例えば

$u$ 委員会は、

$v$ 委員会とは

$C$ ,

$D$ ,

$E$ さんが、

$y$ 委員会とは

$A$ ,

$B$ さんが、

$z$ 委員会とは

$A$ ,

$B$ ,

$C$ ,

$E$ さんが重なっていますので

$v$ ,

$y$ ,

$z$ と隣接させます。他の委員会についても隣接関係を設定すると次のグラフができます。

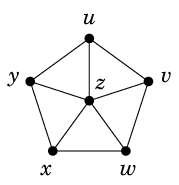
このグラフは

$W_6$ ですから彩色数は 4 で、次のように点彩色できました。

色番号を時間帯と考えて会議は 4 コマで設定できることになります。

4.　彩色数の上限についての定理

Th.12　

$G$ の頂点の次数の最大値を

$\rho$ とすると

$\chi(G) \leqq \rho+1$ .

証明　頂点数についての帰納法で示します。
　頂点

$v$ を 1 つ取り

$G'=G-v$ とおくと、

$G'$ の頂点の次数も

$\rho$ 以下ですから帰納法の仮定により

$\chi(G') \leqq \rho +1$ . です。そこで、

$G'$ を

$\rho+1$ 色以下で点彩色しておくと、

$v$ の隣接点は

$\rho$ 個以下なので

$\rho+1$ 色のうち

$v$ に塗れる色がまだ残っています。(証明終)

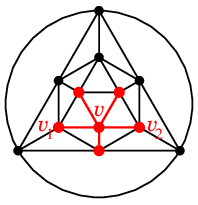
　例えば次のグラフでは

$\rho=4$ です：

	→		→
$G$		$G'=G-v$ を 5 色で点彩色しておく		$v$ には 5 が塗れる

$G$ が完全グラフでないときはこの上限はあと 1 つ下げることができます。

Th.13（Brooks）　

$\rho$ は Th.12 のとおりとし、さらに

$\rho \geqq 3$
$G \not \cong$ 完全グラフ

であれば

$\chi(G) \leqq \rho$ .

　証明はテキストの §18 にありますが、とても長いので省略します。

5.　平面的グラフの場合

Lemma 14　

$G$ が平面的グラフであれば、

$G$ のいくつかの辺を縮約したグラフ

$G'$ も平面的である。

証明　縮約とは辺を 1 点に潰すことなので、

$G$ を平面グラフとして描画しておけば

$G'$ にも辺の交差はありません。（クラトフスキーの定理を使ってもわかります。）(証明終)

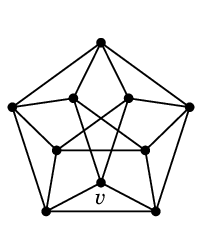
Th.15　

$G$ が平面的グラフならば

$\chi(G) \leqq 5$ .

証明　これも頂点数についての帰納法で示します。
　第９回 Cor.19 より

$G$ は次数

$5$ 以下の頂点

$v$ を持ちます。

$\rho(v) \leqq 4$ のとき
Th.12 と同様に、 $G-v$ を $5$ 色以下で点彩色しておけば $v$ に塗れる色が残っています。
$\rho(v) = 5$ のとき
$G$ は平面的なので $K_5$ は含みません。従って $v$ の 5 つの隣接点 $v_1$ , $\cdots$ , $v_5$ のうち $v_1$ と $v_2$ は隣接しないと仮定できます。 $G$ を $vv_1$ , $vv_2$ の 2 辺で縮約したグラフを $G'$ としましょう。 L'a 14 より $G'$ は平面的ゆえ、帰納法の仮定より 5 色以下で点彩色できます。そこで $G$ の $v$ 以外の頂点に $G'$ で塗った色を割り当てると、 $v_1$ と $v_2$ は隣接しないのでここまでは点彩色の条件を満たしており、 $v_1$ , $\cdots$ , $v_5$ には 4 色以下しか使っていませんので $v$ に塗れる色も残っています。(証明終)

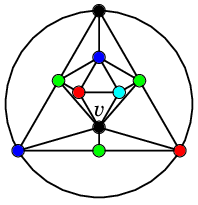
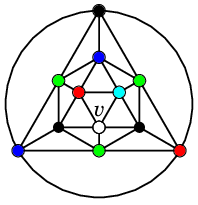
正二十面体グラフでは次のようになります。（本当に色を塗ってみました。）

→ →

$G$ $G' =G\backslash \{vv_1,vv_2\}$
を 5 色で点彩色しておく $v$ に塗れる色が残っている

　平面性がかなり強い条件なので、彩色数も低く抑えてられいる、ということです。

6.　地図の彩色

Def.16　橋の無い連結平面グラフを「地図」と呼ぶ。

　橋の両側は同じ国なので、橋は国境として考えなくていい、という定義です。

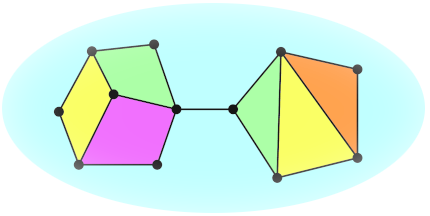
Def.17　地図

$G$ の面に色を割り当て、隣接する面同士は別の色になるようにすることを「G の面彩色」という。

Th.18（四色定理）　全ての地図は 4 色以下で面彩色できる。（ Appel and Haken, 1976）

　印刷業者さんの間では経験則として知られていて、提唱されたのは 1852 年。最初に証明されるまでに 120年以上が費やされました。 Appel と Haken の証明はコンピュータを用いて「2000個弱の可約配置からなる不可避集合」を作る、というもので、コンピュータを用いた証明のさきがけでした。

　地図の面彩色ではこんなことも言えます。

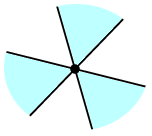
Th.19　地図

$G$ については、2 色で面彩色できることと、オイラーグラフであることが同値である。

証明　

$\Rightarrow)$ 　ひとつの頂点にはその次数個の面が集まっていますので、 2 色で面彩色できるためには次数は偶数でなければなりません。

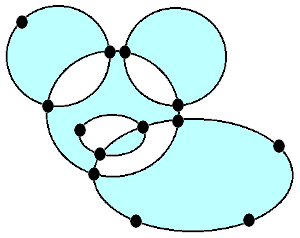
$\Leftarrow)$ 　オイラーサーキットを閉路に分割し、それをベン図だと思って XOR 式に塗り分ければ宜しい。(証明終)

7.　注意

彩色数を求める問題は NP 完全問題ですので高速なアルゴリズムはありません。
コンピュータで彩色数を計算するための道具として「彩色多項式」という多項式が定義されます。グラフ描画ツールにも使っていますし、興味深い内容ですので例年扱っているのですが、今年度は授業が１回少なくなってしまいましたので割愛します。余裕のある諸君は是非 §21 を勉強してください。

宿題

ここから download
提出期限：急がなくていいですが、一応次回を目安に。
提出方法：スキャンするか写メを撮るかして、shiota＠is.kochi-u.ac.jp 宛に送信してください（＠は小文字）。上手く送信できない人は個別に相談してください。
宿題を複数回分まとめて提出されると見落とす危険があります。 多少面倒でも１回分ずつ送信してください。 ... 現在３科目担当していて合計130名程度の受講生がおりますのでご配慮ください。

戻る

	→		→
$G$		$G' =G\backslash \{vv_1,vv_2\}$ を 5 色で点彩色しておく		$v$ に塗れる色が残っている