組合せとグラフの理論（塩田）　2020年度 第10回


今日のテーマ

  • 双対（そうつい）グラフ
　平面グラフには、それと対をなす「双対グラフ」が存在し、お互いが表と裏の関係になっています。 その描き方と性質を勉強しましょう。

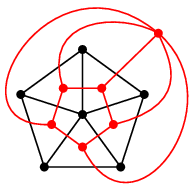
1.　双対グラフの定義

　まずは定義から。
Def.1　平面グラフ $G=(V,E)$ に対し、$\newcommand{\as}{^{\ast}}$ その双対グラフ（幾何学的双対グラフ）$G\as=(V\as, E\as)$ を次のように定める。
  1. $G\as$ の頂点は $G$ の面のことである。
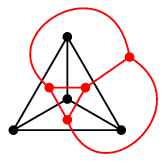
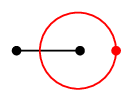
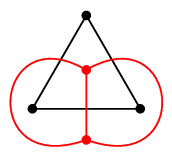
  2. $G$ の面 $\alpha$ と $\beta$ が辺を共有するとき、 $G\as$ の頂点として $\alpha$ と $\beta$ を隣接させる。
　何のこっちゃ、と思うかもしれませんが、描き方を聴くと意味が分かります。
描き方　
  1. $G$ の各面に点をひとつずつ打つ
  2. 隣り合う面に打った点同士を、境界辺をまたぐ辺で結ぶ。
※　$G$ の辺が交差していないことが前提です。ここ大事！
Ex.2　正四面体グラフの双対グラフ（赤いグラフが双対グラフです。）
→ →
グラフの外側もひとつの面ですから忘れないように。
やってみよう　Ex.2 をまねて立方体グラフの双対グラフを描いてみましょう。
やってみよう　車輪グラフ $W_6$ の双対グラフも描いてみましょう。
Rem.3　$G \cong H$ であっても、 平面グラフとしての描画が異なると $G\as \not\cong H\as$ となることがある。（今日の宿題を参照。）
Rem.4　$G$ が単純グラフであっても、$G\as$ にはループや多重辺ができることがある。
     
Th.5　
  1. $G$ が連結な平面グラフであれば $G\as$ もそうである。
  2. $G$, $G\as$ の頂点数、辺数、面数をそれぞれ $n$, $n\as$, $m$, $m\as$, $f$, $f\as$ とすると、
    $n\as = f$, $\quad m\as = m$, $\quad f\as = n$.
証明　(1)　$G\as$ が平面グラフになることは描き方よりわかります。 $G\as$ の連結性は「 $G$ の面が順番にたどれる」ということです。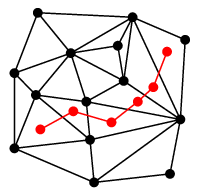
(2)　$n\as = f$ であることは Def.1 (1) より。 $m\as = m$ であることは描き方の (2) より。 すると、 $G$, $G\as$ についてオイラーの公式が成り立つことから
$n- m + f = 2 = n\as - m\as + f\as = f - m + f\as$
よって $f\as = n$. (証明終)

　双対グラフの双対グラフは自分自身に戻ります。
Th.6　$G$ が連結な平面グラフであれば $(G\as)\as \cong G$.
証明　図では双対グラフに赤色を使って述べていきます。
  1. $G\as$ の面 $\alpha\as$ の境界辺の 1 つを $e\as$、 $e\as$ がまたいでいる $G$ の辺を $e=uv$ とすると、 $u$, $v$ のどちらか一方は面 $\alpha\as$ の中にあります。
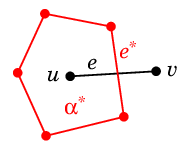
  2. つまり $G\as$ の各面 $\alpha\as$ には $G$ の頂点 $u$ が 1 つ以上あります。
  3. 2° の対応を $\varphi:\alpha\as \mapsto u$ と表すと、 $f\as=n$ ですから $\varphi$ は一対一対応であることがわかります。
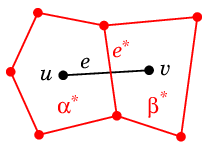
  4. 3° の対応によって $\varphi(\alpha\as)=u$, $\varphi(\beta\as)=v$ であるとします。 このとき、
    $u$ と $v$ が $G$ で隣接していること
       $\Leftrightarrow$ $\ e=uv$ が $G$ の辺であること
       $\Leftrightarrow$ $\ e\as$ が $\alpha\as$ と $\beta\as$ の境界であること
       $\Leftrightarrow$ $\ \alpha\as$ と $\beta\as$ は $(G\as)\as$ の頂点として隣接すること
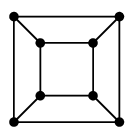
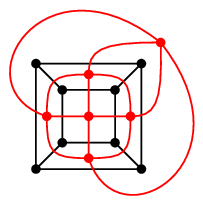
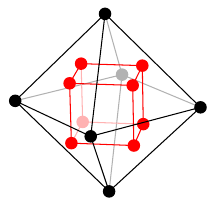
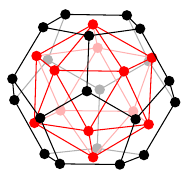
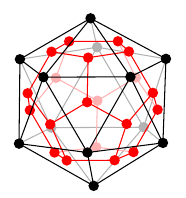
    となるので、$\varphi$ は $(G\as)\as$ と $G$ の隣接関係を写し合います。(証明終)

2.　プラトングラフの双対性

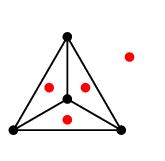
　プラトングラフの双対グラフは次のように描くことができます。
  1. 立体として考える（球面上に描くことと本質的に同じ）
  2. 各面の中心に点をひとつずつ打つ
  3. 隣り合った面に打った点同士の間に辺を描く
するとこんな絵になります。
    
     
　正多面体の双対グラフは再び正多面体グラフになっていますが、これは描き方から必然的にそうなるのです。定理としてまとめると、
Th.7　
  • 正四面体グラフの双対グラフは正四面体グラフである。（自己双対、と言います。）
  • 立方体グラフと正八面体グラフは互いに双対である。
  • 正十二面体グラフと正二十面体グラフは互いに双対である。
　前回の頂点数、辺数、面数の表
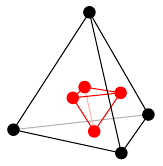
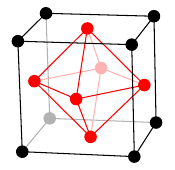
$n$ $m$ $f$ $n-m+f$
正四面体グラフ4642
立方体グラフ81262
正八面体グラフ61282
正十二面体グラフ2030122
正二十面体グラフ1230202
が対称的になっているのはこの定理が理由です。

3.　閉路とカットセットの双対性

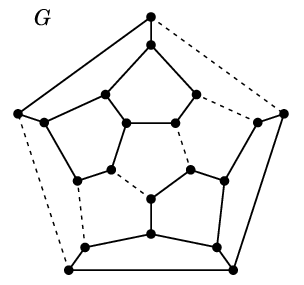
　$G$ を連結な平面グラフ、$G\as$ をその双対グラフとし、辺の一対一対応
$e$ $\longleftrightarrow$ $e\as$
によって $G$, $G\as$ の辺の部分集合 $C$, $C\as$ が対応しているとします。
$C$ $\longleftrightarrow$ $C\as$
このとき
Th.8　
  1. $C$ が $G$ のカットセットであること $\ \Leftrightarrow\ $ $C\as$ が $G\as$ の閉路であること。
  2. $C$ が $G$ の閉路であること $\ \Leftrightarrow\ $ $C\as$ が $G\as$ のカットセットであること。
証明　 (1) の $\Rightarrow$ )　 $C$ がカットセットならば $G-C$ の頂点 ( $=$ $G\as$ の面 ) は 2 つのグループに分かれますから、 $C\as$ はそのグループ同士の境界線を含みます。 カットセットの極小性から $C\as$ は丁度その境界線に一致し、境界線は閉路ですので $C\as$ は閉路になります。
　例えば正十二面体グラフ $G$ とその双対グラフ $G\as$ の場合、
図の点線部分のようにカットセット $C$ を取ると、
対応する $C\as$ は図の赤い辺たちとなり、閉路になります。
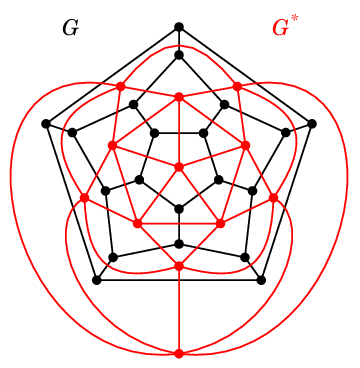
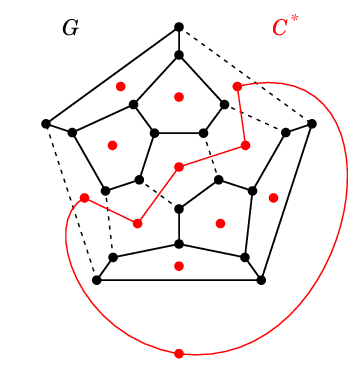
(2) の $\Rightarrow$ )　 $C$ が閉路なら $C$ の内側にも外側にも面（ $=$ $G\as$ の頂点 ) があるので、 $G\as-C\as$ は 2 つの連結成分に分かれます。 $C\as$ の辺を 1 本でも元へ戻すと連結になりますので $C\as$ はカットセットです。
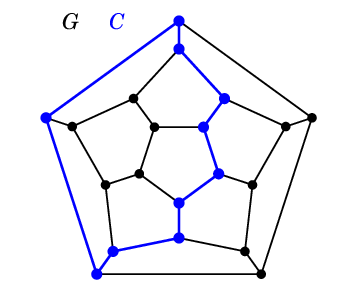
　(1) と同じグラフ $G$ で図の青い部分のように閉路 $C$ を取ると、
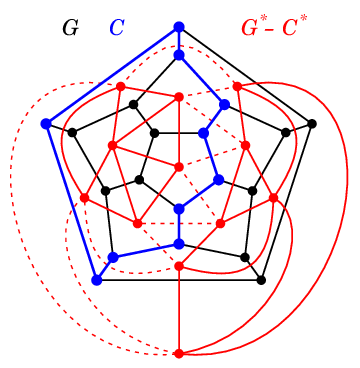
赤い点線の部分が $C\as$ となり、$G\as-C\as$ を 2 つの連結成分に分けるカットセットとなっています。
(1), (2) の $\Leftarrow$ )　は $G$ と $G\as$ を逆にすると言えます。(証明終)

4.　双対グラフの使いどころ

　双対グラフは、プラトングラフの例のように理論的に興味深いという他に、例えば次のような応用を持ちます。
Ex.9　第１回で紹介しました四色問題は面を塗り分ける問題でした。 面を塗り分けることはそのままでは表現しにくいのですが、 双対グラフの頂点を塗り分ける（点彩色と言います）ことに言い換えると処理し易くなります。
Ex.10　カットセットはコンピュータネットワークの強度（辺連結度）にかかわる重要な概念ですが、 扱いにくいものです。 もしネットワークが平面的であれば、双対グラフの閉路に読み替えられて、 第７回に扱った閉路部分空間で制御することが可能となります。

宿題

  • ここから download
  • 提出期限：急がなくていいですが、一応次回を目安に。
  • 提出方法：スキャンするか写メを撮るかして、shiota＠is.kochi-u.ac.jp 宛に送信してください（＠は小文字）。 上手く送信できない人は個別に相談してください。
  • 宿題を複数回分まとめて提出されると見落とす危険があります。 多少面倒でも１回分ずつ送信してください。 ... 現在３科目担当していて合計130名程度の受講生がおります。 課題チェックの作業量をちょっと想像してみてください。

戻る