組合せとグラフの理論(塩田) 2020年度 第8回
今日のテーマ
- 最短路問題
- 郵便配達員問題
- 最小連結子問題
- 巡回セールスマン問題
-
今日は有名なグラフ問題を4つ扱います。
その名の通り最短路を求める最短路問題をはじめ、
それぞれが何某かの最適化問題です。
今まで習ったアルゴリズムを応用して
高速なアルゴリズムで解けるものもあれば、
そうでないものもあります。
1. 重み付きグラフ
今日扱うグラフは全て連結で、かつ、次に定義する「重み付きグラフ」であるとします。
Def.1 全ての辺 $e$ に「重み」と呼ばれる数 $w(e)$ が設定されているグラフを
「重み付きグラフ」と呼ぶ。
Ex.2 重みは辺の横に書き入れます。
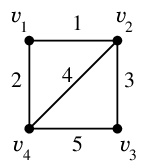
この重み付きグラフは、隣接行列では
$\left(
\begin{array}{cccc}
0 & 1 & 0 & 2 \\
1 & 0 & 3 & 4 \\
0 & 3 & 0 & 5 \\
2 & 4 & 5 & 0 \\
\end{array}
\right)$
のように表します。
(多重辺ありの場合と紛らわしいようですが、
普通、重みと多重辺は同時には使いませんので、状況で判断します。)
※ 例えば地図を表すグラフであれば、重みとして
などを設定することができて、
「最短時間でたどり着けるルート」ということが考えられるようになります。
2. 最短路問題
Def.3 重み付きグラフ $G$ 内の歩道や部分グラフに対して、
それが含む辺の重みの合計を、
その歩道や部分グラフの重みと定める。
最短路問題 連結な重み付きグラフ $G$ において、
出発点 $S$ と到着点 $T$ を指定したとき、
重み最小の $S$-$T$道を求めよ。
※ 重みが距離の場合がまさしく最短路ですので、それにちなんだネイミングです。
Rem.4 目先の利益しか考えない「欲張りアルゴリズム」では最短路問題は解けない。
次のグラフで欲張りさんが最短の $S$-$T$ 道を探すとしましょう。
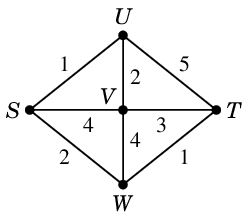
出発点 $S$ から直接見えるのは $U$, $V$, $W$ で、
このうち一番近い $U$ へ進みます。
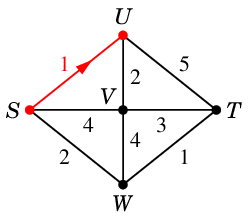
$U$ から直接見えるのは $S$, $V$, $T$ で、
$S$ へ戻っては意味が無いので、
$V$ と $T$ の近い方の $V$ へ進みます。
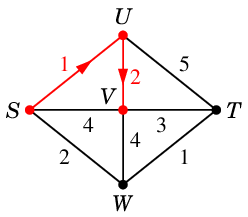
$V$ からは全ての頂点が見えていて、
$S$ や $U$ へは戻らないので、
$W$ と $T$ の近い方の $T$ へ進み、ゴールします。
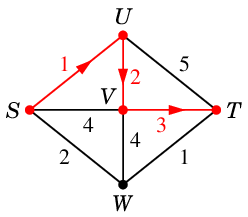
しかし本当の最短路は $S \rightarrow W \rightarrow T$ ですから、
欲張りさんのアルゴリズムでは見つけられません。
最短路問題には決定版のアルゴリズムがあります。
Algorithm 5(ダイクストラ法)
- 入力:連結な重み付きグラフ $G$ と、出発点 $S$、到着点 $T$
- 出力:最短の $S$-$T$ 道
- 全ての頂点 $v$ に仮ラベル $\ell(v)$ を発行する。
- 出発点は $\ell(S)=0$
- $S$ 以外の頂点 $v$ は $\ell(v)=\infty$
- 親を覚えるためのリストを宣言する。
- 仮ラベルが最小のものを永久ラベルに昇格させる。
ただし候補が複数あるときは、番号(アスキーコード、アルファベット順 etc.)が一番小さいもののみ昇格させる。
- $\ell(T)$ が永久ラベルに昇格したら、$T$ から逆順に親をたどって $S$-$T$ 路を出力し終了する:
$S$ $\rightarrow$ $\cdots$ $\rightarrow$ ($T$ の親の親) $\rightarrow$ ($T$ の親) $\rightarrow$ $T$
- 今昇格した頂点 $x$ の全ての未昇格な隣接点 $v$ 全てに対し、
$\ell(x)+w(xv) \lt \ell(v)$
であれば
$\ell(v)$ $\leftarrow \ell(x)+w(xv)$, $\quad$ ( $v$ の親 ) $\leftarrow x$
と更新する。
- 3°に戻る。
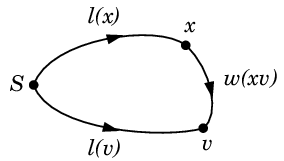
永久ラベルは確定した最短距離を表していて、ステップ 5°は、
- $\ell(x)+w(xv)$ $=$ (確定した最短の $S$-$x$ 道と辺 $xv$ を経て $v$ に至る道の距離)
- $\ell(v)$ $=$ (今まで見つかっている最短の $S$-$v$ 道の距離)
を比較しています。
Ex.6 次のグラフでダイクストラ法を実行し、$A$ から $F$ への最短路を求めてみましょう。
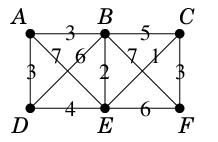
以下、永久ラベルには〇を付け、永久ラベルに昇格したばかりの頂点を青色で示すことにします。
また、最初の仮ラベル $\infty$ は省略し、
親子関係は赤い線で示しています。
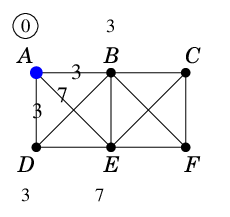 |
まず出発点の $\ell(A)$ を永久ラベルに昇格させます。
$A$ の隣接点 $B$, $D$, $E$ の仮ラベルを、$A$ からの距離 3, 3, 7 に更新します。 |
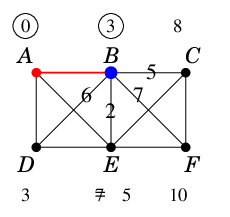 |
仮ラベル 3 の頂点のうち、アルファベット順で若い方の $\ell(B)$ を永久ラベルに昇格させます。
$B$ の未昇格な隣接点の仮ラベルを 5°に従って更新します。
特に $E$ は $B$ を経由したルートの方が短いので仮ラベルが 7 から 5 に減ります。 |
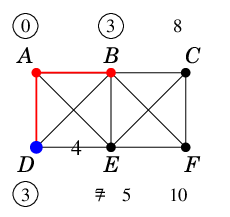 |
最小の仮ラベル $\ell(D)$ を永久ラベルに昇格させます。
$D$ の未昇格な隣接点は $E$ のみですが、
$D$ を経由しても近くならないので仮ラベルは更新されません。 |
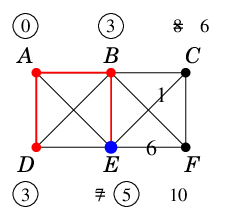 |
最小の仮ラベル $\ell(E)$ を永久ラベルに昇格させます。
$C$ は $E$ を経由したルートの方が短いので仮ラベルが 8 から 6 に減ります。 |
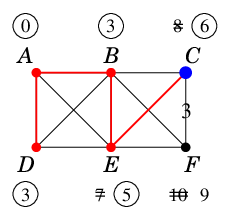 |
最小の仮ラベル $\ell(C)$ を永久ラベルに昇格させます。
$F$ は $C$ を経由したルートの方が短いので仮ラベルが 10 から 9 に減ります。 |
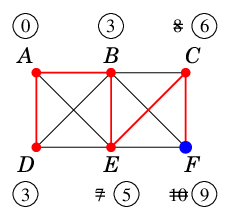 |
到着点の $\ell(F)$ が永久ラベルに昇格して終了します。
最短路は $A$ $\rightarrow$ $B$ $\rightarrow$ $E$ $\rightarrow$ $C$ $\rightarrow$ $F$ となりました。 |
※ 慣れてくれば、グラフの絵ひとつにラベルを書くだけで作業できるようになります。
Prop.7 全ての辺の重みが 1 であれば、ダイクストラ法は幅優先探索(到着点が探索されるまで)に等しい。
「永久ラベルに昇格した頂点」が幅優先探索の探索点に当たり、
$\ell(v)$ が $\infty$ から更新された瞬間に $v$ はキューに登録されます。
3. 郵便配達員問題
郵便配達員問題 連結な重み付きグラフ $G$ において、
全ての辺を 1 回以上通る閉じた歩道で重み最小のものを求めよ。
※ 郵便配達員さんは全ての道を通って配達をして、最後は郵便局へ帰って来なければなりません。
その最短ルートを求める問題です。
Prop.8 $G$ がオイラーグラフであれば、オイラーサーキットが郵便配達員問題の解である。
証明 定義より。(証明終)
Prop.9 $G$ がオイラーグラフでない半オイラーグラフであれば、
以下のアルゴリズムにより郵便配達員問題の解が求まる。
- 奇数次数の 2 頂点を $u$, $v$ とする。
- Alg.5 を用いて最短の $u$-$v$ 道 $P$ を求める。
- $P$ 上の辺を二重化したグラフを $G'$ とする。
- $G'$ のオイラーサーキットを出力する。
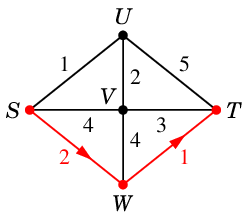
Ex.10 次のグラフで郵便配達員問題を解きましょう。
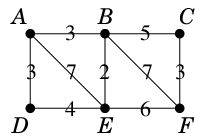
奇数次数の頂点は $A$, $F$ の 2 個なので、
最短の $A$-$F$ 道を求めると
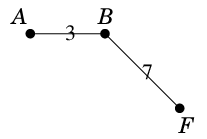
となります。
この辺を二重化すると図のように全ての頂点の次数が偶数になり、
そのオイラーサーキットが解になります。
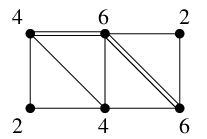
では奇数次数の頂点が 4 個のときはどうでしょうか。
Ex.11 次のグラフで郵便配達員問題を解きましょう。
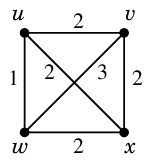
やはり何本かの辺を二重化してオイラーグラフにします。
今度は奇数次数の頂点が 4 個ですので、
2 本以上の辺を二重化する必要があります。
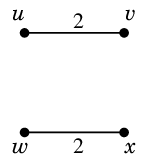 |
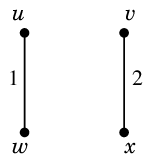 |
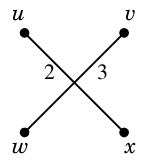 |
(1) $uv$ と $wx$ を二重化
$\Rightarrow$ 重みは 4 増える |
(2) $uw$ と $vx$ を二重化
$\Rightarrow$ 重みは 3 増える |
(3) $ux$ と $vw$ を二重化
$\Rightarrow$ 重みは 5 増える |
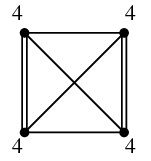
(2) の場合が重みが最小になるので、
$uw$ と $vx$ を二重化したグラフでオイラーサーキットを求めます。
これを一般化すると
Prop.12 連結な重み付きグラフ $G$ において、
奇数次数の頂点が $u$, $v$, $w$, $x$ の 4 個であれば、
以下のアルゴリズムにより郵便配達員問題の解が求まる。
- Alg.5 を用いて
- 最短の $u$-$v$ 道と、最短の $w$-$x$ 道
- 最短の $u$-$w$ 道と、最短の $v$-$x$ 道
- 最短の $u$-$x$ 道と、最短の $v$-$w$ 道
を求める。
- 1°の 3 通りのうち、距離の合計が最小の場合の、最短路上の辺を二重化したグラフを $G'$ とする。
- $G'$ のオイラーサーキットを出力する。
Rem.13 奇数次数の頂点が多数あるときは、
Prop.12 1°のような組み合わせの場合の数が膨大になるので、
後日勉強する「マッチング」のアルゴリズムを応用することになります。
4. 最小連結子問題
最小連結子問題 連結な重み付きグラフ $G$ において、重み最小の全域木 $T$ を求めよ。
※ コンピュータ間のケーブルの敷設コストが重みであれば、
最小コストでとりあえず通信ができる状態にしよう、ということです。
この問題も決定版のアルゴリズムがあります。
Algorithm 14(クラスカル法)
- 入力:連結な重み付きグラフ $G$
- 出力:重み最小の全域木 $T$
- ( 辺集合として ) $T$ の初期値は $\emptyset$ とする。
- $n=$ ( $G$ の頂点数 ), $\,j = 1$ とおく。
- $T$ に付加しても閉路を作らない辺のうち、重み最小のものを $e_j$ とする。
- $T$ に $e_j$ を付加する。
- $j \leftarrow j + 1$.
- $j=n$ ならば $T$ を出力して終了。そうでなければ 3°に戻る。
Ex.15 次のグラフでクラスカル法を実行してみましょう。
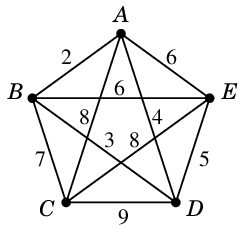
重みの小さい順に辺をソートして考えます。
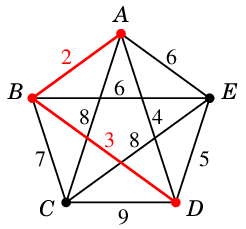
- 重み $2$: $AB=e_1$
- 重み $3$: $BD=e_2$
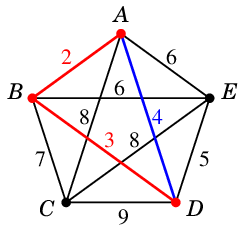
- 重み $4$: $AD$ ... 閉路を作るので不可
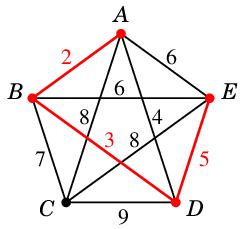
- 重み $5$: $ED=e_3$
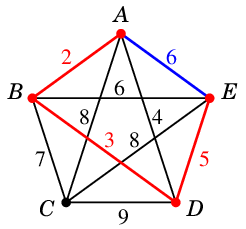
- 重み $6$: $AE$ ... 閉路を作るので不可
- 重み $6$: $BE$ ... 閉路を作るので不可
- 重み $7$: $BC=e_4$
(1) 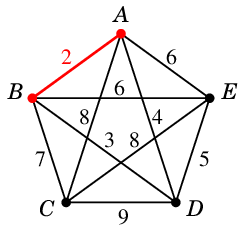 →
(2)
→
(2)  →
→
(3)  →
(4)
→
(4)  →
→
(5)  →
(6)
→
(6) 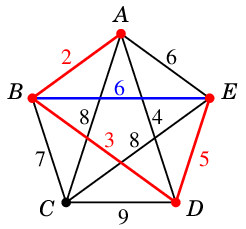 →
→
(7) 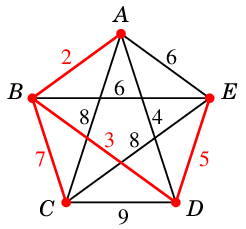 で終了。
※
で終了。
※ 絵はひとつあれば十分作業できます。
Alg.14 の証明 $T$ の重み $w(T)$ の最小性を示します。
- $S$ を $G$ の任意の全域木
- $e_k$ を、$S$ に含まれない $T$ の辺のうち番号最小のもの
とします。
- $S$ に $e_k$ を付加したグラフ $S_{tmp}$ には閉路 $C$ が 1 つだけあります。( 第6回 Th.5 )
- $T$ は閉路を含まないので、$T$ に含まれない $C$ の辺 $f$ が存在します。
- $S_{tmp}$ から $f$ を除去したグラフを $S'$ とおくと、これは再び $G$ の全域木になります。
- $S'$ は $e_1$, $e_2$, $\cdots$, $e_k$ を含むことに注意してください。
- Alg.12 3°より $w(e_k) \leqq w(f)$ ですから、
$w(S') = w(S) + w(e_k) - w(f) \leqq w(S)$
- $S$ から $S'$ を作った操作を繰り返すと全ての $e_j$ を含む $T$ ができるので、
$w(T) \leqq \cdots \leqq w(S') \leqq w(S)$
従って $w(T)$ が重み最小となります。(証明終)
5. 巡回セールスマン問題
巡回セールスマン問題 重み付きハミルトングラフ $G$ において、重み最小のハミルトンサイクル $C$ を求めよ。
※ セールスマンが全ての顧客(頂点)を訪問して会社へ戻る最短ルートを求める問題です。
有名な問題なのですが、これは厄介な代物です:
Rem.16
- 残念ながら、巡回セールスマン問題には高速なアルゴリズムは見つかっていません。
- 巨大なグラフでは、膨大な時間を掛けて最適解を求めるより、
- 遺伝的アルゴリズム
- シミュレーテッド・アニーリング法
などを使って「ましな解」を見つけて実行する方が賢いやり方です。
デモ動画
mp4 が再生可能なブラウザでご覧ください。
宿題
- ここから download ... 6月12日 9:50am 以前に download した人は昨年度の問題だったと思います。download し直してください。
- 提出期限:急がなくていいですが、一応次回を目安に。
- 提出方法:スキャンするか写メを撮るかして、shiota@is.kochi-u.ac.jp 宛に送信してください(@は小文字)。
上手く送信できない人は個別に相談してください。
- 宿題を複数回分まとめて提出されると見落とす危険があります。
多少面倒でも1回分ずつ送信してください。
... 現在3科目担当していて合計130名程度の受講生がおります。
課題チェックの作業量をちょっと想像してみてください。
戻る


















 →
(2)
→
(2)  →
→ →
(4)
→
(4)  →
→ →
(6)
→
(6)  →
→ で終了。
で終了。




