組合せとグラフの理論(塩田) 2020年度 第7回
今日のテーマ
-
辺が多いほどグラフの中にはたくさんの閉路があります。
その閉路たちは一見無秩序に存在するように思われますが、
実は線形構造を持っていて、統制することが可能です。
今日はまず線形代数のツボを簡単に復習し、
それをもとに閉路たちを統制する方法を勉強します。
さらに、電気回路への応用についても述べます。
(教科書では p.47 演習問題 6.8, pp.62-63, pp.77-78 の内容です。)
1. 線形代数のツボ
線形代数ではベクトル空間(=線形空間)というものを学びました。
ベクトル空間の公理という何やらややこしいものがありましたが、
もっとシンプルに考えましょう。
大雑把な定義
- ベクトルとは
を持つものである。
- ベクトルの集合をベクトル空間と呼ぶ。
約束ごとがシンプルなので、世の中の色んな所にベクトルの構造(=線形構造)が潜んでいて、
それらはぜーんぶ線形代数の知識で処理できてしまうのです。
ベクトル空間ストーリー
- 有限次元のベクトル空間には「基底ベクトル」と呼ばれるベクトルの組
$v_1$, $v_2$, $\cdots$, $v_n$ がある。
- ベクトル $v$ に、$v=c_1v_1+c_2v_2+\cdots c_nv_n$
を満たす数ベクトル $\left(\begin{array}{c}c_1 \\ \vdots \\ c_n \\ \end{array}\right)$ を対応させることで、
全てを数値化することができる。(基底ベクトルが座標軸を定める。)
-
数ベクトルとして表現できれば、あとは行列計算すればよい。
例えば多項式や関数も、$f(x)+g(x)$ で加法が、$cf(x)$ でスカラー倍が定義できますのでベクトルです。
この考え方は「応用数学」や「数値解析」の授業でまた出てきます。
2. 2元体 $\mathbb{F}_2$
ベクトルに対してただの数のことを「スカラー」と呼びます。
線形代数を習い始めたころは実数がスカラーで、
固有値の勉強をする頃になると複素数も使います。
行列計算をするときに、数として要求されることは何かと考えて次の定義に至ります:
Def.1 加減乗除の四則演算ができる数の集合を「体(たい)」と呼ぶ。
この観点から、実数の集合は「実数体」、複素数の集合は「複素数体」と呼ばれ、
実数をスカラーと考えるベクトルは「実ベクトル」あるいは「実数体上のベクトル」というように呼びます。
ここで、情報科学にとって大切な体を導入します。
Def.2 $0$ と $1$ の 2 つしか要素を持たない集合に、
次のように加減乗除を定義した体 $\mathbb{F}_2=\{\,0,1\,\}$ を 「2元体」と呼ぶ。
|
$\begin{array}{|r|cc|}
\hline
a \ b & 0 & 1 \\\hline
0 & 0 & 1 \\
1 & 1 & 0 \\
\hline
\end{array}$
|
$\begin{array}{|r|cc|}
\hline
a \ b & 0 & 1 \\\hline
0 & 0 & 1 \\
1 & 1 & 0 \\
\hline
\end{array}$
|
$\begin{array}{|r|cc|}
\hline
a \ b & 0 & 1 \\\hline
0 & 0 & 0 \\
1 & 0 & 1 \\
\hline
\end{array}$
|
$\begin{array}{|r|c|}
\hline
a \ b & 1 \\\hline
0 & 0 \\
1 & 1 \\
\hline
\end{array}$
|
|
$a+b$
|
$a-b$
|
$a \times b$
|
$a \div b$
|
(普通の数と同様、$0$ では割れません。)
法演算を知っている人には、$\bmod 2$ の計算、と言えばわかるでしょうか。
$2=0$, $\quad -x=x$
と思って計算するのが $\mathbb{F}_2$ です。
Rem.3 $\mathbb{F}_2$ を使って設計したシステムは
- $0$, $1$ はビットそのもの
- 加法=減法は XOR(排他的論理和)
- 乗法は AND
ですから容易にハードウェア化できて、計算も高速にできるというメリットがあります。
3. 演算 $\oplus$
では本題に入ります。
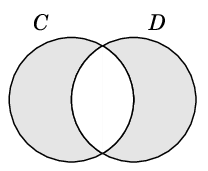
Def.4 グラフ $G$ の辺の部分集合 $C$, $D$ に対して
$C \oplus D = C$ XOR $D$
と定める。
$C \oplus D = (C \cup D) - (C \cap D)$
と書いても同じもので、ベン図では次の色付きの部分です。
Th.5 $C$, $D$ がともに $G$ の閉路であれば、
$C \oplus D$ はいくつかの閉路を合わせたものになる。
(正確に言うと「閉路の辺集合」と言うべきですが、ルーズにしゃべります。)
証明 部分グラフとして $C \oplus D$ 上の頂点の次数は $2$ か $4$ ですので、
第5回の
Th.3 より各連結成分はオイラーグラフであり、
第4回の
Prop.3 よりそれは閉路に分割できます。(証明終)
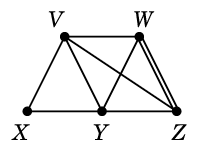
Ex.6 グラフ
$G=$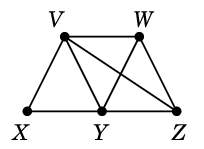
において
$C=$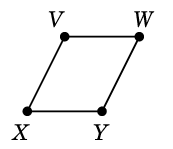 $D=$
$D=$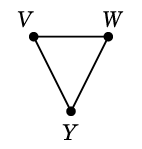
としたとき、$C \oplus D$ を求めましょう。まず $C$ と $D$ を重ねて描き、
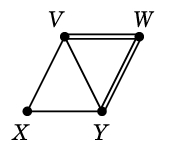
二重辺を消せば出来上がりです:
$C \oplus D=$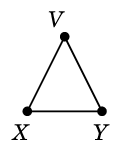
Th.7($\oplus$ の結合律) 3つの辺集合 $B$, $C$, $D$ について
$B \oplus ( C \oplus D) = (B \oplus C) \oplus D$
証明 $n$ 変数の XOR の真偽値は
- 奇数個の変数が真 $\Rightarrow$ 真
- 偶数個の変数が真 $\Rightarrow$ 偽
ゆえ、$\oplus$ の順番には依らない。(証明終) ... ベン図では次の色付きの部分です。
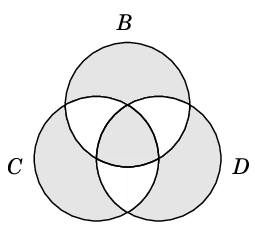 ※
※ ここから、$\oplus$ を一種の「加法」だと考えることにします。すると
Th.8(加法単位元) 空集合 $\emptyset$ は「ゼロ」の役割を持つ:
$C \oplus \emptyset = \emptyset \oplus C = C$, $\quad\forall C$
Th.9(2倍はゼロ) $C \oplus C$ は「 $C$ の2倍」と考えられ、
$2 C = C \oplus C = \emptyset$, $\quad\forall C$
証明 いずれも定義より。
4. 閉路部分空間 $W(G)$
これもまず定義から。
Def.10 $G$ 内の閉路たちから $\oplus$ で作り出せる辺の部分集合全ての集合を $W(G)$ と表し、
「$G$ の閉路部分空間」と呼ぶ。$\emptyset$ も $W(G)$ の要素のひとつとする。
Rem.11 閉路それ自身も全て $W(G)$ の要素である。
Th.12 $W(G)$ は $\mathbb{F}_2$ 上のベクトル空間になる:
- 加法は $\oplus$
- ゼロは $\emptyset$
- 2倍はゼロなので、スカラーは $\mathbb{F}_2$
証明 Th.7-9 より。
$W(G)$ がベクトル空間になることがわかりましたので、あとは「基底ベクトル」をみつけさえすれば
$W(G)$ 内の全てのベクトル、特に $G$ の全ての閉路を統制できることになります。
Def.13 $G$ を連結グラフ、$T$ をその全域木のひとつとする。
$T$ に属さない $G$ の辺 $e$ を $T$ に付加すると閉路 $C_e$ が 1 つだけできる(第6回 Th.5)。
そのような $C_e$ 全ての集合を ${\cal F}(T)$ と表し、「$T$ に関連した基本閉路集合」と呼ぶ。
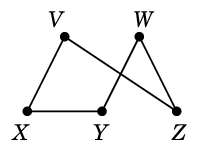
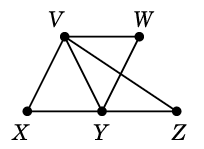
Ex.14 Ex.6 と同じグラフ
$G=$
において、全域木
$T=$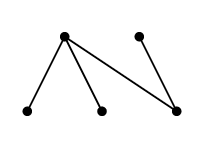
を選んだとしましょう。このとき $T$ に属さない辺は次の $e$, $f$, $g$, $h$ の 4 本です。
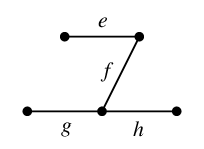
$T$ に $e$ を付加すると、次のように閉路でき(赤い部分)、これが $C_e$ です。
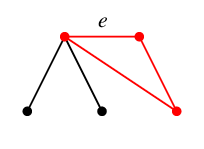
同様に $T$ に $f$ を付加してできる閉路が $C_f$,
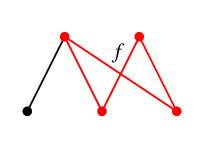
$T$ に $g$ を付加してできる閉路が $C_g$,
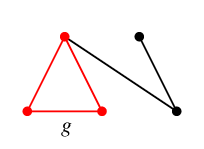
$T$ に $h$ を付加してできる閉路が $C_h$ です。
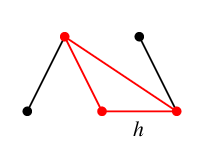
結局、$T$ に関連した基本閉路集合 ${\cal F}(T)$ は
となります。
Th.15 ${\cal F}(T)$ は $W(G)$ の基底になる。すなわち
- 全ての閉路は、基本閉路と $\oplus$ で作ることができる。
- $\dim W(G) = m - n + 1$. ( ただし、$G$ の頂点数を $n$, 辺数を $m$ とする。)
証明 (1) 基本閉路 $C_e$, $C_f$, $\cdots$ を係数 1 で足し合わせると、
$C_e \oplus C_f \oplus \cdots = \{\,e,f,\cdots\,\} \neq \emptyset$
であり、これは基本閉路たちが一次独立であることを意味しています。
そして、任意の閉路 $C$ は次の
Alg.16 によって基本閉路の和として表すことができます。
(2) 次元とは基底ベクトルの個数のことであり、それは $T$ に属さない $G$ の辺の本数でしたから
$\dim W(G) =$ ( $G$ の辺数 ) $-$ ( $T$ の辺数 ) $=m - (n - 1)$.
(証明終)
Algorithm 16
- 入力:$G$ の閉路 $C$
- 出力:$C$ を基本閉路の和として表す表し方
- $T$ に属さない $C$ の辺を $e$, $f$, $\cdots$, $h$ とする。
- $C_e \oplus C_f \oplus \cdots C_h$ を出力する。
証明 $D=C_e \oplus C_f \oplus \cdots C_h$ とおくと、
$e$, $f$, $\cdots$, $h$ は全て $C$ と $D$ に 1 回ずつ含まれますので、$C \oplus D$ には含まれません。
すなわち $C \oplus D$ は $T$ の辺の部分集合になります。
Th.5 から $C \oplus D$ は 閉路に分けられるはずですが、$T$ は閉路を含みませんので、結局
$C \oplus D=\emptyset$. よって $C = -D = D$.
(証明終)
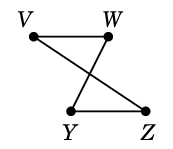
Ex.17 Ex.14 の状況
$G=$ $T=$
$T=$
で
Alg.16 を実行してみます。入力を
$C=$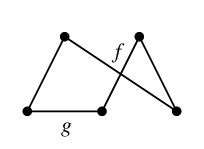
とします。このとき $T$ に属さない $C$ の辺は $f$, $g$ の 2 本です。
$C_f=$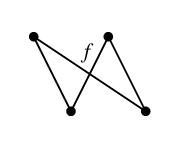 と
$C_g=$
と
$C_g=$
を重ねて描くと
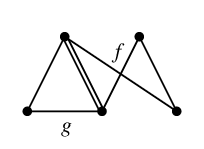
二重辺を消して
$C_f \oplus C_g=$

$C$ になりましたね。
やってみよう Ex.17 の状況で、今度は
$C'=$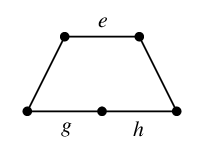
を入力として
Alg.16 を実行してみましょう。
答え
$T$ に属さない $C'$ の辺は $e$, $g$, $h$ の 3 本です。
$C_g=$ $C_h=$
$C_h=$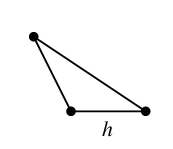 $C_e=$
$C_e=$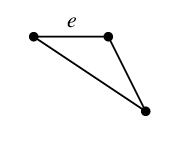
を重ねて描くと
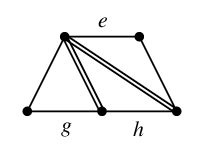
二重辺を消して
$C_e \oplus C_g \oplus C_h=$

$C'$ になりましたね。
5. 電気回路への応用
まずは教科書 p.77 の図を見てください。
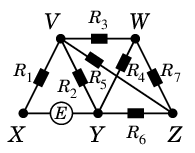
- $R_j$ は各抵抗の抵抗値を表します。
- $i_j$ は各配線の電流量を表します。( 矢印の方向を+とします。)
- $E$ は起電力です。
- 上手に描けていませんが、$VZ$ と $WY$ は交差していないと思ってください。
問題18 $E$ と $R_j$ ( $j=1,2,\cdots$ ) の値を決めたとき、$i_j$ ( $j=1,2,\cdots$ ) の値を求めよ。
この手の問題を解くときに用いるのが
キルヒホフの法則
- 各頂点での電流の総和は $0$ である。
- 各閉路で、電源の電圧の和 $=$ ( 抵抗値 $\times$ 電流量 ) の和、が成り立つ。
(i) は、各頂点で、流入する電流量と流出する電流量が釣り合う、ということです。
(ii) は、電流が抵抗を流れると、( 抵抗値 $\times$ 電流量 ) だけの電圧降下をもたらし、
閉路を一周すると、その電圧降下と供給される電圧が釣り合う、ということです。
Ex.19 3 つの閉路
$C_1=$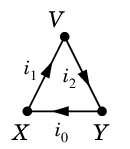 $C_2=$
$C_2=$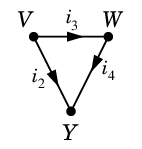 $D=$
$D=$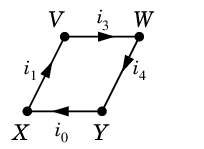
について (ii) 式を書き下すと
$\begin{array}{llll}
C_1 &\!\!\!:&\! R_1i_1 + R_2i_2=E & \cdots\ (1)\\
C_2 &\!\!\!:&\! R_3i_3 + R_4i_4-R_2i_2=0 & \cdots\ (2)\\
D &\!\!\!:&\! R_1i_1 + R_3i_3+R_4i_4=E & \cdots\ (3)\\
\end{array}$
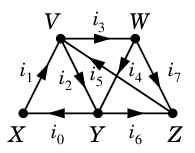
電気回路を表すグラフを $G$ として
Algorithm 20(問題18 の解法)
- $G$ の全域木 $T$ をひとつ求める。
- $T$ に関連した基本閉路集合 ${\cal F}(T)$ を求める。
- (i) の式を各頂点について書く。
- (ii) の式を ${\cal F}(T)$ の各閉路 について書く。(ここ大事!)
- 3-4°の式を $i_j$ たちの連立一次方程式として解く。
(ii) の式を ${\cal F}(T)$ の各閉路についてだけ書けばよい理由は次の命題です。
Prop.21 閉路たちが
$D=C_1 \oplus C_2 \oplus \cdots \oplus C_s$
の関係にあれば
( $D$ についての (ii) 式 ) $=$ ( $C_j$ についての (ii) 式 ) の和
が成り立つ。
任意の閉路は基本閉路の和として表せますので、
その閉路についての (ii) 式は基本閉路についての (ii) 式から自動的に出てくる、という訳です。
Ex.19 では確かに $D=C_1 \oplus C_2$ に従って (3) $=$ (1) $+$ (2) となっていますね。
Rem.22 実際には (i) の式は頂点のうち 1 つだけは省けます。
その理由は、他のすべての頂点で電流の出入りが釣り合っているので、
自動的に最後の頂点でも釣り合ってしまうのです。
宿題
- ここから download
- 提出期限:急がなくていいですが、一応次回を目安に。
- 提出方法:スキャンするか写メを撮るかして、shiota@is.kochi-u.ac.jp 宛に送信してください(@は小文字)。
上手く送信できない人は個別に相談してください。
- 宿題を複数回分まとめて提出されると見落とす危険があります。
多少面倒でも1回分ずつ送信してください。
... 現在3科目担当していて合計130名程度の受講生がおります。
課題チェックの作業量をちょっと想像してみてください。
戻る





 $D=$
$D=$


 $D=$
$D=$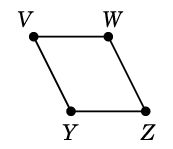














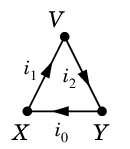 $C_2=$
$C_2=$ $D=$
$D=$