1. 木
まずは木の定義から。
Def.1
- 閉路を持たない連結無向グラフを「木」と呼ぶ。
- 閉路を持たない無向グラフを「林」と呼ぶ。言い換えれば、林とは木の和である。
Ex.2
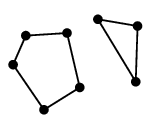
頂点数 5 の木は同型の意味で 3 種類あります:
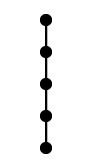
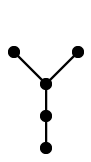
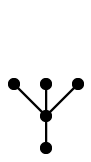
この 3 つを合わせてひとつのグラフと思うと林になります。
Ex.3 次のような二分木はトーナメント表でおなじみでしょう。
基本的なデータ構造としてもよく目にするはずです。
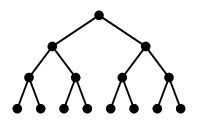
Rem.4 ランダムな木を描くのは簡単です:
- 頂点をひとつ描く
 を継ぎ足してゆく
を継ぎ足してゆく
木は重要な構造ですので、木である条件をいろいろ言い換えておきましょう。
Th.5 頂点数 $n$ のグラフ $T=(V,E)$ について、
次の条件は全て同値である:
- $T$ が木であること
- $T$ は閉路を持たず、辺数 $=n-1$
- $T$ は連結で、辺数 $=n-1$
- $T$ は連結で、全ての辺が橋である
- 任意の 2 頂点 $u$, $v$ $\in V$ に対して、$u$-$v$道が 1 本だけ存在する。
- $T$ は閉路を持たないが、$T$ にどんな辺を付加して閉路が 1 つだけできる
Lemma 6 $e$ を $G$ の辺とする。このとき
- $e$ が橋である
$\Leftrightarrow$ $e$ を含む閉路は無い
$\Leftrightarrow$ $G-e$ は $G$ より連結成分が 1 つだけ多い
- $e$ を含む閉路が 2 つあれば、$e$ を含まない閉路もある
証明の要点 (1) $e$ を含む閉路が無ければこんな感じ:
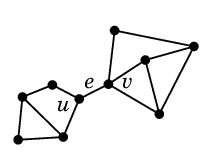
| $\Rightarrow$ |
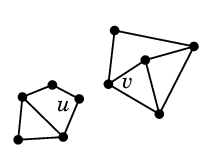
|
| $G$ | | $G-e$ |
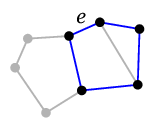
逆に $e=uv$ を含む閉路が有ればこんな感じです:
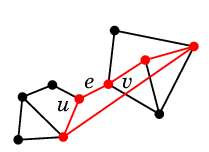
|
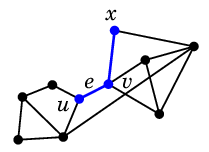
|
|
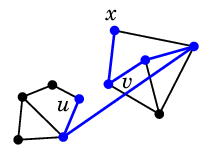
| $e$ を含む閉路があれば |
$e$ を通る $u$-$x$ 道も |
$e$ を通らない $u$-$x$ 道に
取り換えられる |
(2)
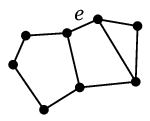
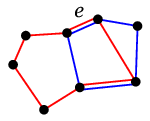
$e$ を含む閉路が 2 つあれば、
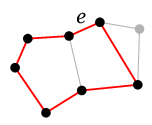 $\phantom{\longrightarrow}$
$\phantom{\longrightarrow}$
重ねて描いておいて二重辺を削除すれば $e$ を含まない閉路たちが残ります。
 $\longrightarrow$
$\longrightarrow$
(証明の要点終)
Th.5 の証明 (1) ⇒ (2) 辺 $e$ をひとつ取ります。
L'a 6 より $e$ は橋で、
$T-e$ は閉路を含まないので 2 つの木 $T_1$, $T_2$ の和になります。
すると帰納法の仮定から
( $T$ の辺数 ) $=$ ( $T-e$ の辺数 ) $+1$
$=$ ( $T_1$ の辺数 ) $+$ ( $T_2$ の辺数 ) $+1$
$=$ ( $T_1$ の頂点数 $-1$ ) $+$ ( $T_2$ の頂点数 $-1$ ) $+1$
$=n-1$
(2) ⇒ (3) $T$ は閉路を持たないので林、すなわち木の和です。
その木の本数を $k$ 本とすれば、(1) ⇒ (2) は既に証明しましたので
( $T$ の辺数 ) $=n-k$.
これが $n-1$ と等しいということは $k=1$、すなわち $T$ は連結になります。
教科書にはこの後 (3) ⇒ (4) ⇒ (5) ⇒ (6) ⇒ (1) の証明が書いてあります。
読んでおいてください。(証明以下省略)
4. 幅優先探索、深さ優先探索
教科書では p.79 で簡単に書いてありますが、大事なアルゴリズムですので時間を掛けてやりましょう。
どちらも「根 ( root )」と呼ばれる頂点を与えて、その根から木を伸ばしてゆきます。
Algorithm 11(幅優先探索、BFS = Breadth-First-Search )
- 入力:連結なグラフ $G$ と、その頂点 $v$
- 出力:$v$ を根とする $G$ のBFS木 $T$
- $v$ を要素とするキュー $Q=\{\,v\,\}$ を作り、 $T$ の初期値は $v$ 一点からなる木とする。
- $Q$ の先頭から $x$ を取り出し、$x$ の未探索な隣接点のすべてを、番号の小さい順に
$y_1$, $y_2$, $\cdots$, $y_s$
とする。
- $Q$ の最後尾に $y_1$, $y_2$, $\cdots$, $y_s$ をこの順で追加し、
$T$ には辺 $xy_1$, $xy_2$, $\cdots$, $xy_s$ をすべて追加する。
- $Q$ が空(くう)リストになれば $T$ を出力して終了。そうでなければ 2°へ戻れ。
Ex.12 まずは二分木の場合に、チョー丁寧に動作を確認してみましょう。
次の図で $v=0$ を根として幅優先探索を実行します。
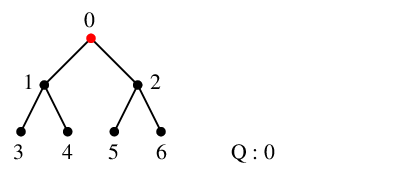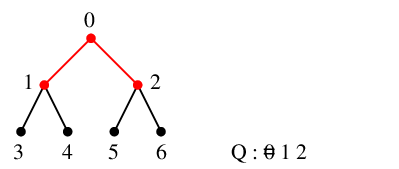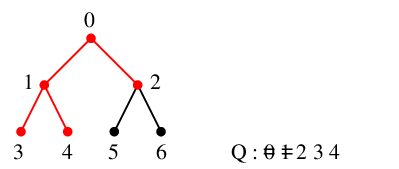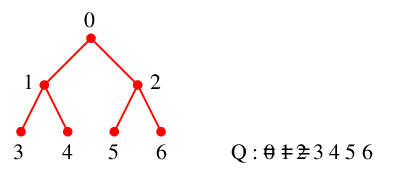
最初は、キューが $Q=\{\,0\,\}$, 赤い部分が $T$ です。
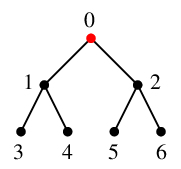
$x=0$ を $Q$ から取り出し、これを探索点(青い点)とします。 一旦 $Q$ は空になります。
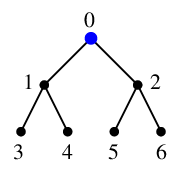
$x=0$ の隣接点 $1$, $2$ はどちらも未探索ですから $y_1=1$, $y_2=2$ になり、
$T$ には辺 $01$ と $02$ を追加、$Q=\{\,1,2\,\}$ になります。
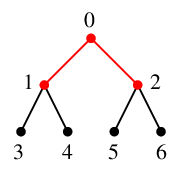
$x=1$ を $Q$ の先頭から取り出し、これを探索点とします。 $Q=\{\,2\,\}$ になります。
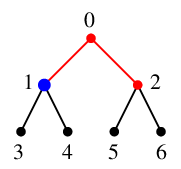
$x=1$ の隣接点 $0$, $3$, $4$ のうち未探索なのは $y_1=3$, $y_2=4$ の 2 つで、
$T$ には辺 $13$ と $14$ を追加、$Q=\{\,2,3,4\,\}$ になります。
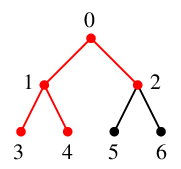
$x=2$ を $Q$ の先頭から取り出し、これを探索点とします。 $Q=\{\,3,4\,\}$ になります。
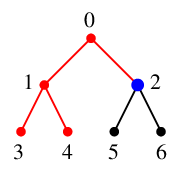
$x=2$ の隣接点 $0$, $5$, $6$ のうち未探索なのは $y_1=5$, $y_2=6$ の 2 つで、
$T$ には辺 $25$ と $26$ を追加、$Q=\{\,3,4,5,6\,\}$ になります。
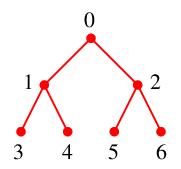
未探索点が無くなりましたので人間がやるときはここでおしまいです。
(アルゴリズム的にはこのあと、$3$, $4$, $5$, $6$ を $Q$ から取り出して $Q$ が空になって終了します。)
Rem.13(
ここ大事!)自分が探索点 $x$(青い点)に立っていて、
$x$ の隣接点までしか見ることができない、というイマジネーションを働かせてください。
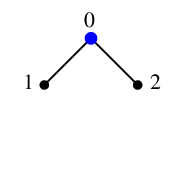
Ex.12 ではそれぞれの場面で
 |
|
 |
|
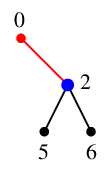 |
| $x=0$ のとき |
|
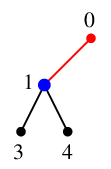
$x=1$ のとき |
|
$x=2$ のとき |
しか見えていなくて、探索済みの赤い点以外の、黒い点たち全てへ
幅広く木を伸ばす、
と考えます。
※ 慣れてくれば、キューを横に書くだけで作業できるようになります。
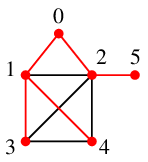
Ex.14 もうひとつ木ではないグラフで、もっとラフにやってみます。やはり $v=0$ を根とします。
根 $v=0$ から探索を開始します。
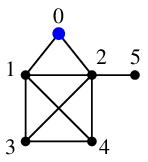
探索点 $0$ から未探索点 $1$, $2$ が見えますので、
$0$ から $1$, $2$ へ辺を伸ばします。
探索点は、キュー $Q=\{\, 1,2\,\}$ の先頭要素 $1$ に移します。
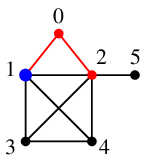
探索点 $1$ から未探索点 $3$, $4$ が見えますので、
$1$ から $3$, $4$ へ辺を伸ばします。
探索点は、キュー $Q=\{\, 2, 3, 4\,\}$ の先頭要素 $2$ に移します。
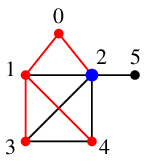
探索点 $2$ から未探索点 $5$ が見えますので、$x=2$ から $5$ へ辺を伸ばして終了です。
次は深さを優先します。
Algorithm 15(深さ優先探索、DFS = Depth-First-Search )
- 入力:連結なグラフ $G$ と、その頂点 $v$
- 出力:$v$ を根とする $G$ のDFS木 $T$
- 空スタック $S=\{\ \}$ を作り、$T$ の初期値は $v$ 一点からなる木とする。また探索点を $x=v$ とする。
- $x$ の未探索な隣接点があれば、そのうち番号の一番小さいものを $y$ とする。
そうでなければ 4°へ。
- $S$ の先頭に $x$ を追加し、$T$ には辺 $xy$ を付加する。探索点を $x=y$ として 2°へ。
- $S$ が空(くう)であれば終了。
そうでなければ $S$ の先頭から $x$ を取り出して探索点とし、2°へ。
Ex.16 再び二分木でチョー丁寧に動作を確認しましょう。
次の図で $v=0$ を根として深さ優先探索を実行します。
最初は、スタック $S$ は空、赤い部分が $T$ です。
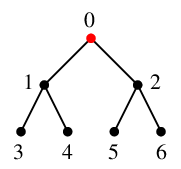
探索点(青い点)は $x=0$とします。
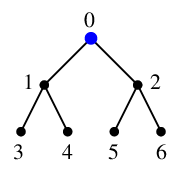
$x=0$ の隣接点 $1$, $2$ のうち番号の小さい方を $y=1$ とします。
$S$ の先頭に $x=0$ を追加し $S=\{\,0\,\}$,
$T$ には辺 $01$ を付加し、探索点を $x=1$ とします。
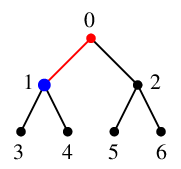
$x=1$ の未探索な隣接点 $3$, $4$ のうち番号の小さい方を $y=3$ とします。
$S$ の先頭に $x=1$ を追加し $S=\{\,1,0\,\}$,
$T$ には辺 $13$ を付加し、探索点を $x=3$ とします。
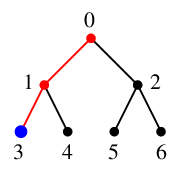
$x=3$ には未探索な隣接点はありませんので、
$S$ の先頭から $x=1$ を取り出し探索点とします。$S=\{\,0\,\}$ になります。
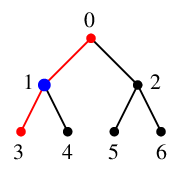
$x=1$ の未探索な隣接点は $4$ のみですので $y=4$ とします。
$S$ の先頭に $x=1$ を追加し $S=\{\,1,0\,\}$,
$T$ には辺 $14$ を付加し、探索点を $x=4$ とします。
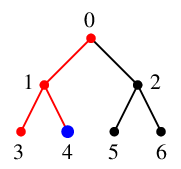
$x=4$ には未探索な隣接点はありませんので、
$S$ の先頭から $x=1$ を取り出し探索点とします。$S=\{\,0\,\}$ になります。
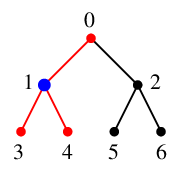
$x=1$ には未探索な隣接点はありませんので、
$S$ の先頭から $x=0$ を取り出し探索点とします。$S=\{\ \}$ になります。
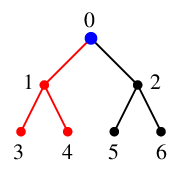
$x=0$ の未探索な隣接点は $2$ のみですので $y=2$ とします。
$S$ の先頭に $x=0$ を追加し $S=\{\,0\,\}$,
$T$ には辺 $02$ を付加し、探索点を $x=2$ とします。
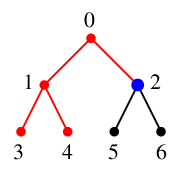
$x=2$ の未探索な隣接点 $5$, $6$ のうち番号の小さい方を $y=5$ とします。
$S$ の先頭に $x=2$ を追加し $S=\{\,2,0\,\}$,
$T$ には辺 $25$ を付加し、探索点を $x=5$ とします。
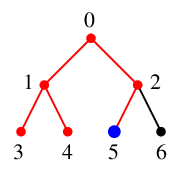
$x=5$ には未探索な隣接点はありませんので、
$S$ の先頭から $x=2$ を取り出し探索点とします。$S=\{\,0\,\}$ になります。
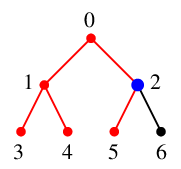
$x=2$ の未探索な隣接点は $6$ のみですので、$y=6$ とします。
$S$ の先頭に $x=2$ を追加し $S=\{\,2,0\,\}$,
$T$ には辺 $26$ を付加し、探索点を $x=6$ とします。
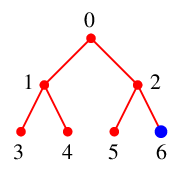
未探索点が無くなりましたので人間がやるときはここでおしまいです。
(アルゴリズム的にはこのあと、$2$, $0$ を $S$ から取り出して $S$ が空になって終了します。)
Rem.17(
ここ大事!) 深さ優先探索の要点は
- $T$ には辺は 1 本ずつしか付加しない。
- 探索点に未探索な隣接点がある限り、深く深く進んでゆく。
- 探索点に未探索な隣接点が無い時は、$T$ の辺をたどって「親」へ戻る。(バックトラック、と言う。)
※ こちらも慣れてくればグラフの絵ひとつだけでできるようになります。
Ex.18 Ex.14と同じグラフで、やはり $v=0$ を根として、ラフにやってみます。
根 $0$ から一番番号の小さい未探索点 $1$ へ進みます。
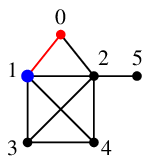
探索点 $1$ から一番番号の小さい未探索点 $2$ へ進みます。
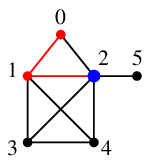
探索点 $2$ から一番番号の小さい未探索点 $3$ へ進みます。
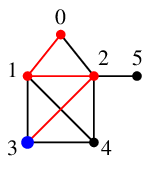
探索点 $3$ から一番番号の小さい未探索点 $4$ へ進みます。
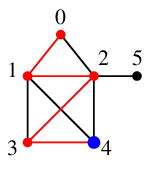
$4$ には未探索な隣接点がありませんので
赤い辺を通って $3$ へバックトラックします。
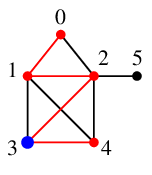
$3$ にも未探索な隣接点がありませんので更に
赤い辺を通って $2$ へバックトラックします。
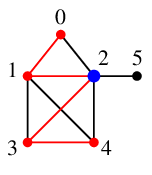
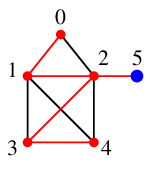
$2$ から $5$ へ進んで終了です。
5. 幅優先探索・深さ優先探索の応用
BFS・DFS を応用したいろんなグラフアルゴリズムを紹介します。
Th.19 BFS木は、根から他の頂点への最短路を与える。
Ex.14 のBFS木は

でした。根 $0$ から $1$, $2$ へは距離 $1$, $3$, $4$, $5$ へは距離 $2$ であることを表しています。
Def.20 DFS木においては親子関係が考えられ、根に近い方の頂点を祖先、根から遠い方の頂点を子孫と定める。
Ex.18 のDFS木は
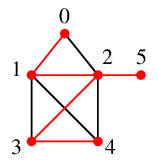
でした。根 $0$ の子は $1$、$1$ の子は $2$、$2$ の子は $3$ と $5$、$3$ の子は $4$ と考えます。
Th.21 DFS木に使われなかった辺は、必ず祖先と子孫をつなぐ。
証明 子孫同士が結ばれていれば祖先にバックトラックしていないはずなので。(証明終)
Th.22 連結グラフ $G$ の頂点 $v$ を根とするDFS木を $T$ とするとき、
$v$ が $G$ のカット点であること $\Leftrightarrow$ $T$ において $v$ の子が 2 人以上いること
証明 Th.21 より $v$ の子孫同士を結ぶ辺は存在せず、
$G-v$ においては $v$ の 2 人の子を結ぶ道が存在しません。(証明終)
非連結なグラフでも幅優先探索・深さ優先探索を行うことができて、
こんな応用もあります:






 $\phantom{\longrightarrow}$
$\phantom{\longrightarrow}$

 $\longrightarrow$
$\longrightarrow$








 を継ぎ足してゆく
を継ぎ足してゆく
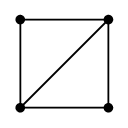 のとき、
次の部分グラフはいずれも $G$ の全域木です。
のとき、
次の部分グラフはいずれも $G$ の全域木です。
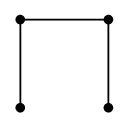 とか
とか
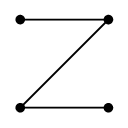 とか
とか
 とか
とか
































