組合せとグラフの理論（塩田）　2020年度第5回

今日のテーマ

オイラーグラフ
ハミルトングラフ

　第１回でお話しした「ケーニヒスベルクの橋渡り」にちなんで、出発点に戻る一筆書きができるグラフをオイラーグラフと呼びます。一筆書きは単なる遊びに留まらず、郵便配達の最短経路を求める最適化問題にも関わっています。前半は、オイラーグラフの判定法や、一筆書きのアルゴリズムについて勉強します。

　全ての辺を１回ずつ通って出発点に戻れるのがオイラーグラフであるのに対し、すべての頂点を１回ずつ通って出発点に戻れるグラフをハミルトングラフと言います。これは巡回セールスマン問題に関わっています。後半はハミルトングラフのお話です。

1.　オイラー性

　特に断りがないときは、今日扱うグラフは全て連結であるとします。

Def.1

一筆書きができる無向グラフを半オイラーグラフと呼ぶ。
一筆書きで出発点へ戻れる無向グラフをオイラーグラフと言い、その道順をオイラーサーキットと呼ぶ。

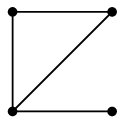
Ex.2

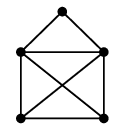
　一筆書きの例として有名なグラフですが、このグラフでは出発点へ戻る一筆書きはできません。すなわち、このグラフは半オイラーグラフですが、オイラーグラフではありません。

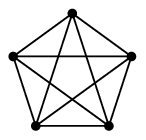
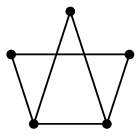
$K_5$ はオイラーグラフです。一つの頂点からまず外側の五角形を書いて、次に内側の星を書けばOKです。

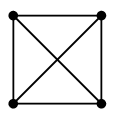
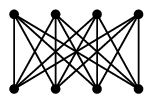
$K_4$ はただの一筆書きもできません。すなわち半オイラーグラフですらありません。

※　それぞれ確かめてみましょう。

　次の定理は第１回の授業でも紹介しました：

Th.3　連結な無向グラフ

$G$ について

$G$ がオイラーグラフであること

$\Leftrightarrow$

$G$ のすべての頂点の次数が偶数であること

※　オイラー性はグラフ全体についてのグローバルな性質ですが、それが次数というローカルな性質で言い換えられるというのはとても興味深いことです。

Lemma 4　

$G$ のすべての頂点の次数が 2 以上であれば、

$G$ には閉路が含まれる。

構成的証明　次のアルゴリズムを実行すれば良い。

Algorithm 5　

テキトーな頂点から小道を作り始める。
来た辺へは戻らずに先へ進み続ける。（これは任意の頂点の次数が 2 以上なので可能です。）
訪問回数が 2 回になった頂点ができた時点で次のような閉路ができる。

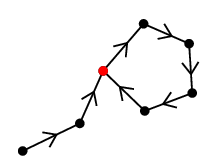
Th.3 の構成的証明　

$\Rightarrow$ )　オイラーサーキットは閉じた小道ですから、第4回の Prop.3 に分割することができます。閉路ではすべての頂点の次数は 2 なので、それらを重ね合わせてできるグラフの頂点の次数は偶数になります。

$\Leftarrow$ )　次のアルゴリズムを実行します：

Algorithm 6　

Alg.5 を用いて閉路 $C_0$ を見つける。
$G-C_0$ の連結成分を $G_1$ , $G_2$ , $\cdots$ , $G_k$ とする。
各 $G_j$ は全ての頂点の次数が偶数である連結グラフゆえオイラーグラフになる。そこで（再帰呼び出しにより） $G_j$ のオイラーサーキット $C_j$ を求る。
$C_0$ と $C_j$ の交点の一つを $v_j$ とする。
$C_0$ 上の 1 点 $v_0$ から $C_0$ をたどり、 $v_j$ へ来たら $C_j$ を迂回してから先へ進む。

Ex.7　図のグラフ

$G$ で Alg.6 を実行しましょう。

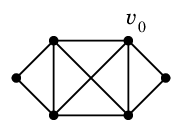
$v_0$ からまず Alg.5 を実行して次の閉路

$C_0$ が得られたとします。

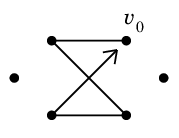
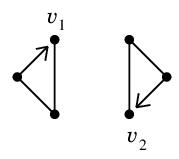
$G-C_0$ の連結成分は 2 つあり、それぞれ図のようなオイラーサーキット

$C_1$ ,

$C_2$ を持ちます。

$C_1$ と

$C_0$ の交点

$v_1$ ,

$C_2$ と

$C_0$ の交点

$v_2$ を取ります。

$C_1$

$C_2$ 　5°に従って次のオイラーサーキットを得ます。

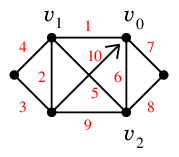
Cor.8　連結な無向グラフ

$G$ について

$G$ がオイラーグラフでない半オイラーグラフあること

$\Leftrightarrow$

$G$ の奇数次数の頂点は 2 個

　証明は次の例を見ればわかるでしょう：

Ex.9　

$K_{2,3}$ では、図の

$u$ ,

$v$ が奇数次数です。

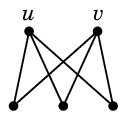
$K_{2,3}$ に辺

$e=uv$ を付加するとすべての頂点の次数が偶数になってオイラーグラフになります。

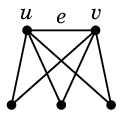
　そのオイラーサーキットを求めて、そこから

$e$ を取り除けば

$K_{2,3}$ の一筆書きになります。

2.　もうひとつのアルゴリズム

Algorithm 10 ( Fleury )　オイラーグラフ

$G$ のオイラーサーキットは次の手順で求まる：

テキトーな頂点から出発する。
現在地の接続辺を 1 つ選んで進む。ただし、橋は、他にたどるべき辺がないときだけ選んで良い。
たどった辺は除去し、孤立点も除去する。
辺が無くなれば終了。そうでなければ 2°へ。

Ex.11　Ex.7 と同じグラフで Alg.10 を実行してみましょう。

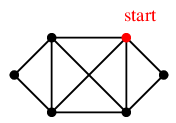
右上の頂点から出発して図のように進んだとします。

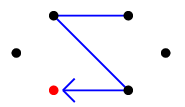
たどった辺（青い辺）を除去すると、残った辺は次の通りです。

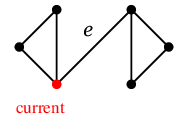
現在地（赤い頂点）には橋

$e$ が接続していますが、他にもたどれる辺があるので、

$e$ は渡らず左の三角形へ進みます。

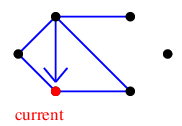
たどった辺を除去し、孤立点も除去します。すると現在地には

$e$ しか接続辺が無いので、今度は

$e$ へ進みます。

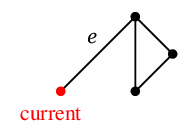
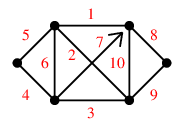
一筆書きの道順はこのようになりました。( 5月25日訂正しました。)

プログラミング上の注意　

Alg.6 には
- 閉路を 1 つ見つけるルーチン Alg.5
- 連結成分へ分解するルーチン
が必要で、また、再帰的アルゴリズムのデメリットとして、メモリを大量に消費します。
Alg.10 は
- 橋かどうかを判定するルーチン
があれば実装できます。塩田のツールでは Alg.10 を用いています。
連結成分への分解、橋の判定は、後日勉強する幅優先探索・深さ優先探索を応用して行います。

3.　ハミルトン性

　今度は、全ての頂点を含む道、あるいは閉路を持つかどうかを考えます。

Def.12　オーダー

$n$ のグラフ

$G=(V,E)$ について、

$P_n$ と同型な部分グラフを持つとき（すなわち全ての頂点を通る道を含むとき）、 $G$ を半ハミルトングラフと言う。
$C_n$ と同型な部分グラフを持つとき（すなわち全ての頂点を通る閉路を含むとき）、 $G$ をハミルトングラフと言う。

それぞれ、その部分グラフを半ハミルトン道、ハミルトンサイクルと呼ぶ。

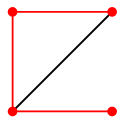
Ex.13　次のグラフはハミルトングラフでしょうか？

答え

答え　赤い部分グラフが半ハミルトン道です。しかし、右下の頂点を含む閉路は存在しないのでハミルトングラフではありません。

答え

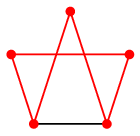
答え　赤い部分グラフがハミルトンサイクルです。
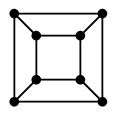
答え

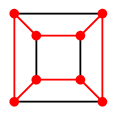
答え　立方体グラフもハミルトングラフです。
答え

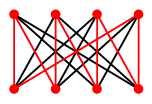
答え　 $K_{n,n}$ ( $n \geqq 2$ ) もハミルトングラフです。ちなみに、 $K_{n,n+1}$ ( $n \geqq 1$ ) は半ハミルトンですが、 $K_{n,n+k}$ ( $n \geqq 1$ , $k \geqq 2$ ) は半ハミルトンにもなりません。

Ex.14　次のグラフも全てハミルトングラフです。

$C_n$ ( $n \geqq 3$ )
$K_n$ ( $n \geqq 3$ )
プラトングラフたち
$Q_k$ ( $k \geqq 2$ )

Rem.15　

ハミルトン性の判定は NP 完全問題ですので、高速なアルゴリズムはありません。（オイラー性の判定が、次数を数えるだけなので瞬時にできることと対照的です。）
テキスト Th.7.1 は「やたらたくさん辺があればハミルトングラフである」という内容ですが、仮定が強すぎるので実社会ではほとんど使えません。
オイラー性は郵便配達員問題に、ハミルトン性は巡回セールスマン問題に関わっています。詳しくは後日。

4.　有向グラフのオイラー性

　有向グラフでは弧の向きに従って一筆書きを考えます。（一方通行が指定されている道路をイメージしてください。）

Def.16　有向グラフの頂点

$v$ に対し、その入出次数とは

入次数 $\mbox{indeg}(v)=$ ( $v$ に入る弧の本数 )
出次数 $\mbox{outdeg}(v)=$ ( $v$ から出る弧の本数 )

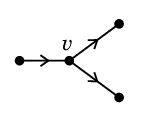
では

$\mbox{indeg}(v)=1$ ,

$\qquad\mbox{outdeg}(v)=2$ と数えます。

Th.17　連結な有向グラフ

$D$ について

$D$ がオイラーグラフであること
$\qquad\Leftrightarrow$ $D$ のすべての頂点 $v$ で $\mbox{indeg}(v)=\mbox{outdeg}(v)$ が成り立つこと

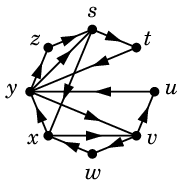証明は無向グラフの場合を若干修正すればできます。ポイントは

有向オイラーサーキットは有向閉路に分けられること
有向閉路では $\mbox{indeg}(v)=\mbox{outdeg}(v)=1$ が成り立つこと
Alg.5, Alg.6 は向きを指定しても成り立つこと

です。

5. 応用

　余裕のある諸君は こちらのプリント もご覧ください。

完全グラフのオイラーサイクル
順列の半ハミルトン道
ドゥブリュエイン列

について書いてあります。

デモ動画

　mp4 が再生可能なブラウザでご覧ください。

オイラーグラフ
- $K_7$ ( 365KB )
- $K_{4,6}$ ( 395KB )
- 正八面体グラフ( 309KB )
- 4次元立方体グラフ( 347KB )
オイラーでない半オイラーグラフ
- $K_{2,5}$ ( 317KB )
- ランダム( 296KB )

宿題

ここから download
提出期限：急がなくていいですが、一応次回を目安に。
提出方法：スキャンするか写メを撮るかして、shiota＠is.kochi-u.ac.jp 宛に送信してください（＠は小文字）。上手く送信できない人は個別に相談してください。
宿題を複数回分まとめて提出されると見落とす危険があります。多少面倒でも１回分ずつ送信してください。 ... 現在３科目担当していて合計130名程度の受講生がおります。課題チェックの作業量をちょっと想像してみてください。

戻る