組合せとグラフの理論(塩田) 2020年度 第4回
今日のテーマ
- グラフの中の道いろいろ
- 道を用いた連結性の定義
- 連結度
今日はまず、グラフの中の「道」について勉強します。
今日で一応の基礎ができるので、次回は一筆書きの話をします。
また後半では、グラフがどの位強く連結であるかを表す「連結度」の勉強をします。
1. グラフの中の道いろいろ
まず、いろいろな種類の道を定義して、そのあとで例を示します。
Def.1
- (1) 歩道 ( walk )
-
隣接する頂点を次々辿ってゆく道筋を「歩道」と呼ぶ。(辿り方には特に制限はありません。)
$v_0 \rightarrow v_1 \rightarrow \cdots \rightarrow v_n$
$v_0$ を始点、$v_n$ を終点と呼ぶ。
- (2) 小道 ( trail )
-
同じ辺は二度通らない歩道のこと。同じ頂点を通ることは許す。
- (3) 閉じた小道
-
始点と終点が等しい小道は「閉じた小道」と呼ぶ。
- (4) 道 ( path )
-
今後、単に「道」と言えば、同じ点を二度通らない小道を指すこととする。
ただし、始点と終点が等しいことだけは許す。
始点が $v$, 終点が $w$ である道は「$v$ から $w$ へ至る道」、「$v$-$w$ 道」などと呼ぶ。
- (5) 閉路 ( cycle )
-
閉じた道を特に「閉路」と呼ぶ。つまり
- 閉路 $=$ 閉じた道 $=$ 閉路グラフと同型な部分グラフ
- 閉じていない道 $=$ 道グラフと同型な部分グラフ
※ なお、教科書によって微妙に用語が違うことがありますので、読んでいておかしいときはその本の定義を見直してください。
次の命題は次回の一筆書きに使います:
Prop.3 閉じた小道 $T$ は閉路に分割できる。
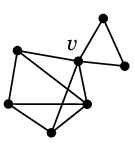
Ex.4 例えば次のグラフの赤線のような閉じた小道 $T$
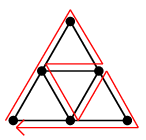
は
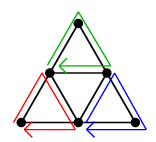 や
や
のように分けることができます。
( 一通りとは限りません。)
Prop.3 の構成的証明 $T$ を
$T:v_0 \rightarrow v_1 \rightarrow \cdots \rightarrow v_n$
とし、$v_0$ から出発して訪問回数が最初に2回になる頂点を
$v_i = v_j$ ( $i \lt j$ )
とします。このとき、
$C:v_i \rightarrow v_{i+1} \rightarrow \cdots \rightarrow v_j$
は $T$ に含まれる閉路になります。$T$ から $C$ を取り除いて
$T':v_0 \rightarrow \cdots \rightarrow v_i \rightarrow v_{j+1} \rightarrow \cdots \rightarrow v_n$
という歩道 $T'$ を作ると、これは $T$ より短い閉じた歩道になります。
帰納法の仮定より $T'$ は閉路に分割できるので、それらと $C$ と合わせれば宜しい。(証明終)
Ex.4 では図の赤い頂点が最初に訪問回数が2回になります。
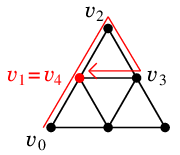
従って $C$, $T'$ は
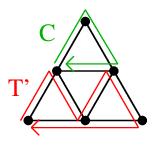
となります。
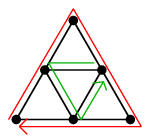
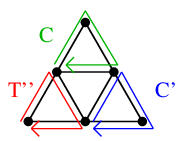
$T'$ に対して「構成的証明」を再帰的に適用すると図の閉路 $C'$ がみつかり、
$T'$ から $C'$ を取り除いた $T''$ が閉路になっているので、これで分割が終了します。
プログラミングのために大切なこと
- プログラミングをするためには、単に可能性を証明するだけでは駄目で、構成的証明が必要です。
- さらに、それが数学的帰納法で書いてあれば、再帰的プログラミングで実装することができます。
2. 道を用いた連結性の定義
Def.5 グラフ $G=(V,E)$ が連結である、とは、任意の2頂点 $u$, $v \in V$ に対して $u$-$v$ 道が存在すること。
これは第3回の
Def.5 の言い換えになっています。
Th.6 $V$ 上の関係 $\sim$ を
$u \sim v$ $\Leftrightarrow$ $u$-$v$ 道が存在すること
と定めれば、$\sim$ は同値関係であり、
$\sim$ による類別が $G$ の連結成分を与える。
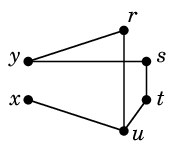
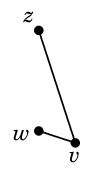
Ex.7 次のグラフ
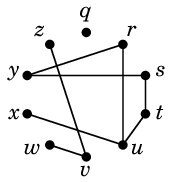
では
$r \sim s \sim t \sim u \sim x \sim y$, $v \sim w \sim z$
となっていて、3つの連結成分が得られます:
復習
- 同値関係とは「同じ」ということの論理的表現で、次の3つの条件を満たす関係でした:
- 対称律:$a \sim a$
- 反射律:$a \sim b$ $\Rightarrow$ $b \sim a$
- 推移律:$a \sim b$ かつ $b \sim c$ $\Rightarrow$ $a \sim c$
- 同値なもの同士をひとつのクラス($=$ 同値類)として分類することが、同値関係の大きな目的です。
- 小学校から習ってきた同値関係として次のようなものがあります:
- 図形の合同関係
- 図形の相似関係
- 整数の合同関係 $x \equiv y \pmod n$
次の定理は、「二部グラフ」という構造を「閉路」を用いて特徴付けます:
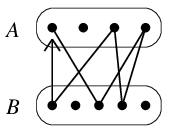
Th.8 単純無向グラフ $G$ について次は同値:
- $G$ が二部グラフであること
- $G$ の任意の閉路が偶数長であること
証明 (1) $\Rightarrow$ (2)
閉路を作るためには2つの頂点集合を数回往復しなければならないので。
(2) $\Rightarrow$ (1)
$G=(V,E)$ の各連結成分が二部グラフであれば $G$ 全体も二部グラフになるので、
以下、$G$ が連結であると仮定して証明します。頂点 $u \in V$ をひとつ固定し、
$A=\{\,v \in V \,|\, $ 最短の $u$-$v$ 道は偶数長 $\,\}$
$B=\{\,v \in V \,|\, $ 最短の $u$-$v$ 道は奇数長 $\,\}$
とおきましょう。$G$ は連結なので $V=A \cup B$ となっています。
$A$ の頂点同士、$B$ の頂点同士は隣接しないことを示します。
もし $A$ の2頂点 $v$, $w \in A$ が隣接すると仮定すると、
最短の $u$-$v$ 道、最短の $u$-$w$ 道と辺 $vw$ の絵はこのような状態になっています:
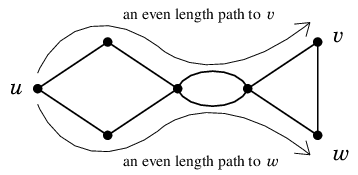
合計で奇数本の辺が描かれていることに注意してください。
ここから二重辺を除去すると
のようにいくつかの閉路が残りますが、辺の本数が奇数ですから、
その中に奇数長の閉路が存在することになり仮定に矛盾します。
$B$ の2頂点 $v$, $w \in B$ が隣接すると仮定しても同様の矛盾が生じますので、
$G$ が二部グラフであることが示されました。(証明終)
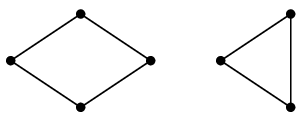
Cor.9 二部グラフは部分グラフとして $C_3$ ( 三角形 ) を含まない。
第2回の
Ex.10 では
$G=$ と
$H=$
と
$H=$ は同型ではない
は同型ではない
と言いましたが、$H$ は完全二部グラフ $K_{3,3}$ と同型なので三角形を含まない、
というところが要
(かなめ)でした。
3. 連結度
連結なグラフ $G=(V,E)$ について、どの位強く連結であるかを数値として表現しましょう。
Def.10
- $e \in E$ に対し、$G-e$ が非連結になるとき $e$ を「橋」と呼ぶ。
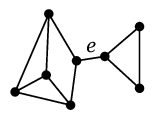 |
→ |
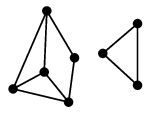 |
| | $G-e$ |
- 辺の部分集合 $F \subset E$ に対し、$G-F$ が非連結になるとき $F$ を「非連結化集合」と呼ぶ。
- 極小な非連結化集合を「カットセット」と呼ぶ。
「$F$ が極小な非連結化集合である」とは、$F$ 自身は非連結化集合であるが、
$F$ のどんな真部分集合も非連結化集合にならない、ということです。
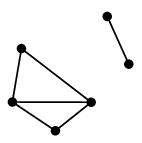
Ex.11 次のグラフ
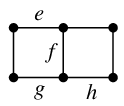
において、
- $F=\{\,e,f,g\,\}$ は非連結化集合です:
$G-F$
しかし、$F$ はカットセットではありません。なぜなら
- $F$ の真部分集合 $F'=\{\,e,g\,\}$ はカットセットです:
$G-F'$
$e$ または $g$ を復活させると連結に戻るので、$F'$ は極小な非連結化集合、つまりカットセットになります。
- $F''=\{\,e,f,h\,\}$ もカットセットです:
$G-F''$
※ カットセットの辺数は一定とは限りません。
Def.12 $G$ の辺連結度とは
$\lambda(G)=$ ( カットセットの辺数の最小値 )
( $\lambda$ はギリシャ文字のラムダ )
例えばコンピュータネットワークを表すグラフにおいては、
カットセットに属する回線が全て切れてしまうと通信ができなくなります。
従って、$\lambda(G)$
が大きいほどネットワークは安全、ということになります。
Rem.13
- 橋 $e$ は1本だけでカットセットになる。
( $G-e$ は非連結、$G$ は連結ゆえ。)
- 橋が存在すること $\Leftrightarrow$ $\lambda(G)=1$.
- Ex.11 では $\lambda(G)=2$.
( 橋は無いので $\lambda(G) \geqq 2$ であり、$F''$ は辺数 2 のカットセットゆえ。)
次は頂点に関する連結度を考えます。
Def.14
- $v \in V$ に対し、$G-v$ が非連結になるとき $v$ を「カット点」と呼ぶ。
 |
→ |
 |
| | $G-v$ |
- 頂点の部分集合 $W \subset V$ に対し、$G-W$ が非連結になるとき $W$ を「分離集合」と呼ぶ。
Ex.15 次のグラフ
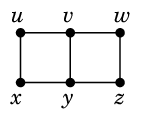
において、
$W=\{\,v,x\,\}$ や $W'=\{\,v,y\,\}$ は分離集合の例です:
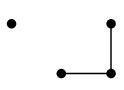 |
|
 |
| $G-W$ | | $G-W'$ |
Def.16 $G$ の連結度とは
$\kappa(G)=$ ( 分離集合の頂点数の最小値 )
( $\kappa$ はギリシャ文字のカッパー )
コンピュータネットワークを表すグラフにおいては、
分離集合に属するサーバが全てダウンしてしまうと通信ができなくなります。
辺連結度と同様に、$\kappa(G)$
が大きいほどネットワークは安全、ということになります。
Rem.17
- カット点 $v$ は1個だけで分離集合になる。
( $G-v$ は非連結、$G$ は連結ゆえ。)
- カット点が存在すること $\Leftrightarrow$ $\kappa(G)=1$.
- Ex.15 では $\kappa(G)=2$.
( カット点は無いので $\kappa(G) \geqq 2$ であり、$W$ は頂点数 2 の分離集合ゆえ。)
Th.18
$\kappa(G) \leqq \lambda(G) \leqq$ ( $G$ の頂点の次数の最小値 )
証明 次数が最小の頂点を $v$、$v$ の接続辺の全てを $W$ とすると、$G-W$ では $v$ が孤立点となって非連結になりますから
$\lambda(G) \leqq v$ の次数
であることがわかります。
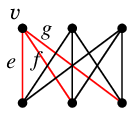 |
→ |
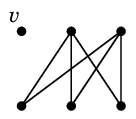 |
| $W=\{\,e,f,g\,\}$ | | $G-W$ |
あとは [7] Bondy-Murty P.37 を見てください。( 教科書末の文献表参照 )
デモ動画
mp4 が再生可能なブラウザでご覧ください。
宿題
- ここから download
- 提出期限:急がなくていいですが、一応次回を目安に。
- 提出方法:スキャンするか写メを撮るかして、shiota@is.kochi-u.ac.jp 宛に送信してください(@は小文字)。
上手く送信できない人は個別に相談してください。
- 宿題を複数回分まとめて提出されると見落とす危険があります。
多少面倒でも1回分ずつ送信してください。
... 現在3科目担当していて合計130名程度の受講生がおります。
課題チェックの作業量をちょっと想像してみてください。
戻る






 と
$H=$
と
$H=$ は同型ではない
は同型ではない


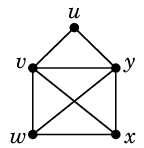
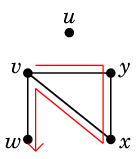
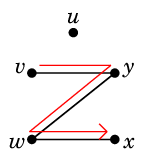
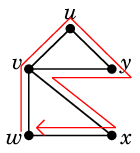
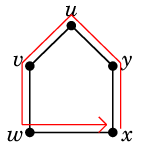
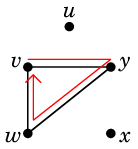
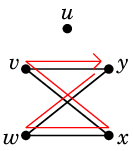 これらは閉路です。
これらは閉路です。
 や
や