組合せとグラフの理論(塩田) 2020年度 第3回
今日のテーマ
- 名前のついているグラフ
- グラフの演算
- 連結性の定義
1. 名前のついているグラフ
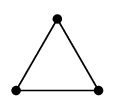
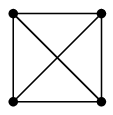
(1) 完全グラフ $K_n$
オーダー $n$ で、全ての頂点が互いに隣接している単純無向グラフのこと。
(2) 空グラフ $N_n$
辺を持たない、オーダー $n$ のグラフのこと。「くうグラフ」と読みます。辺集合が空集合、という意味です。
 |
|
 |
| $N_3$ |
|
$N_4$ |
(3) 正則グラフ
全ての頂点の次数が等しいグラフのこと。(これは固有名詞ではありません。)
その次数が $r$ のとき、$r$-正則グラフと呼んだり、$r$-正則である、と言ったりします。
例えば、
- $K_n$ は $(n-1)$-正則グラフ
- $N_n$ は $0$-正則グラフ
です。
正則グラフの中でも美しくて有名なのが
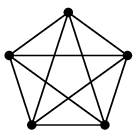
(4) ペテルセングラフ(ピーターセングラフ)
オーダー 10, サイズ 15, 3-正則な次のグラフ:
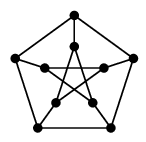
シンプルでありながら、平面的でない、ハミルトングラフではない、など、いろいろな概念の例としてよく使われます。
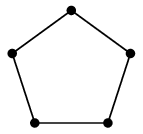
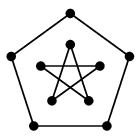
五角形の中に星を描いて内と外をつなげばよいので、自分でも描けるようになりましょう。
 →
→
 →
→

Prop.1 オーダー $n$ の $r$-正則グラフのサイズは $\displaystyle{\frac{rn}{2}}$.
証明 前回の握手補題より
$2$ $\times$ サイズ $=$ 次数の和 $=$ $r \times n$
ゆえ。(証明終)
例えばペテルセングラフでは $n=10$, $r=3$ で $rn/2=15=$ サイズ、になります。
問 $r$ が奇数のとき、$r$-正則グラフのオーダー $n$ は必ず偶数である。なぜか?
次も正則グラフの例です:
(5) プラトングラフ
正多面体の頂点と辺から作ったグラフをプラトングラフと呼びます。5種類あります。
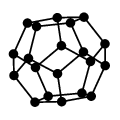 |
|
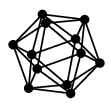 |
| 正十二面体グラフ |
|
正二十面体グラフ |
これらは辺の交差無く描くこともできます:
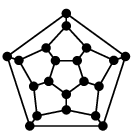 |
|
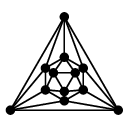 |
| 正十二面体グラフ |
|
正二十面体グラフ |
やってみよう
- 2通りの描き方をした各プラトングラフが同型になっていることを確かめましょう。
- それぞれのオーダーとサイズを数えてみましょう。
(6) 二部グラフ
頂点集合 $V$ が交わりの無い2つの部分集合 $A$, $B$ に分かれ
( $V=A \cup B$, $A \cap B = \emptyset$ )、
$A$ に属する頂点と $B$ に属する頂点の間にしか辺が無いグラフを二部グラフと呼びます。
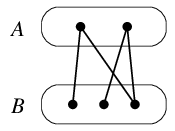
$A$ の頂点同士、$B$ の頂点同士は隣接しない、と言っても同じです。
(7) 完全二部グラフ $K_{m,n}$
上の状況で、特に
- $|\,A\,|=m$, $|\,B\,|=n$
- $A$ の頂点と $B$ の頂点は必ず隣接
となるときを完全二部グラフと呼び、$K_{m,n}$ と表します。
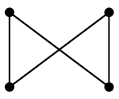 |
|
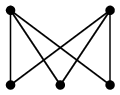 |
| $K_{2,2}$ |
|
$K_{2,3}$ |
(8) 星グラフ
$K_{1,n}$ のことですが、頂点の配置によって星の形に見えるので星グラフと呼びます。
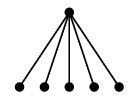 |
|
$\cong$ |
|
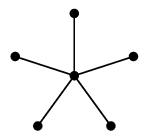 |
| $K_{1,5}$ |
|
|
|
こう描けば星の形 |
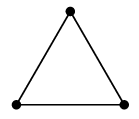
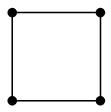
(9) 閉路 $C_n$
$n$ 頂点の、輪の形のグラフです。$n$ 角形の頂点と辺から作ったグラフ、と言っても同じです。
 |
|
 |
| $C_3$ |
|
$C_4$ |
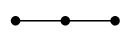
(10) 道グラフ $P_n$
$n$ 頂点の、一直線の形のグラフです。
 |
|
 |
| $P_3$ |
|
$P_4$ |
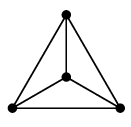
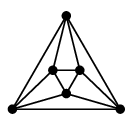
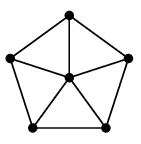
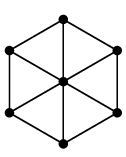
(11) 車輪グラフ $W_n$
$n$ 頂点の、文字通り車輪の形のグラフです。
真ん中にも点があるので $W_n$ は $n-1$ 角形の車輪です。
 |
|
 |
| $W_6$ |
|
$W_7$ |
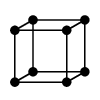
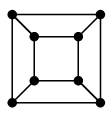
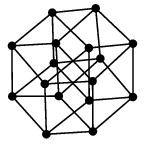
(12) $k$ 次元立方体グラフ $Q_k$
$k$ 次元立方体の頂点と辺から作ったグラフです。
少しわかりにくいかもしれませんが、こういう定義をします:
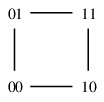
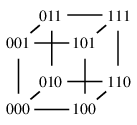
- 長さ $k$ のビット列を頂点とする。
- 1 ビットだけ違うビット列同士を辺で結ぶ。
$k=2,\,3$ の場合を描いてみると、
 |
|
 |
| $Q_2 \cong C_4$ |
|
$Q_3 \cong$ 立方体グラフ |
問 4 次元立方体グラフ $Q_4$ はイメージできますか?
※ $Q_k$ の中での距離は、符号理論で用いる「ハミング距離」と同じもので、信号の誤り訂正能力に関わる重要な概念です。
2. グラフの演算
(1) 和
単に並べて描くことです。記号は $\cup$ を用います。


$C_3 \cup C_4$
(2) 頂点の除去
グラフ $G$ から頂点 $v$ を除去したグラフを $G-v$ と表します。
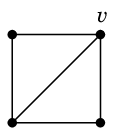 |
|
$\longrightarrow$ |
|
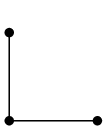 |
| $G$ |
|
|
|
$G-v$ |
注意 消した頂点の接続辺も全て消します。
(3) 辺の除去
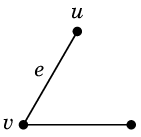
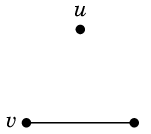
グラフ $G$ から辺 $e$ を除去したグラフを $G-e$ と表します。
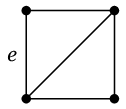 |
|
$\longrightarrow$ |
|
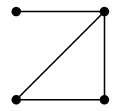 |
| $G$ |
|
|
|
$G-e$ |
注意 こちらは、孤立点ができても、それを消してはいけません。
 |
|
$\longrightarrow$ |
|
 |
| $G$ |
|
|
|
$G-e$ |
コンピュータネットワークで言えば、$u$ はケーブルを切られて困っているコンピュータ、ということになります。
困っている人を切り捨ててはいけない、という意味でしょうか。
(4) 辺の縮約
少し複雑な操作ですが、とても役に立つ演算ですので覚えてください。
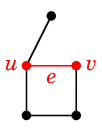
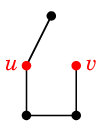
グラフ $G$ から辺 $e=uv$ を縮約したグラフを $G \backslash e$ と表し、
次の操作で定義します:
- $e$ を除去します。
- $u$ と $v$ を重ねて描きます。
 |
|
$\longrightarrow$ |
|
 |
|
$\longrightarrow$ |
|
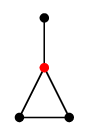 |
| $G$ |
| | | | | | |
$G \backslash e$ |
※ 辺を 1 点につぶすイメージです。
注意 縮約により多重辺が生じることがありますが、普通はそれを 1 本に減らします。(状況にも依りますが。)
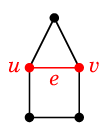 |
|
$\longrightarrow$ |
|
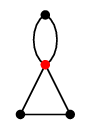 |
|
$\longrightarrow$ |
|
 |
| $G$ |
| | | | | | |
$G \backslash e$ |
(5) 複数の頂点の除去、辺の除去、辺の縮約
$G-\{\,u,v,w\,\}$, $G-\{\,e,f,g\,\}$, $G\backslash\{\,e,f,g\,\}$ のように表します。
また、頂点の部分集合 $W=\{\,u,v,w\,\}$ を用いて $G-W$ というような書き方もします。
Rem.2 除去・縮約は
で活躍します。頂点や辺が減ることで、帰納法の仮定が使えたり、再帰的アルゴリズムが有限の深さで終了する、という仕組みです。
詳しくは後日。
(6) 補グラフ
単純グラフ $G$ に対し、
頂点の「 隣接する / しない 」関係を逆転させたグラフを $G$ の補グラフと呼び、$\overline{G}$ と表します。
 |
|
$\longrightarrow$ |
|
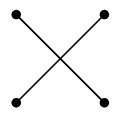 |
| $C_4$ |
| | |
$\overline{C_4}$ |
※ $K_4$ から $C_4$ の辺を全て除去したグラフが $\overline{C_4}$ になるイメージです。
Ex.3 $\overline{C_5}$ は $C_5$ と同型になる。( $C_5$ は自己補対である、と言います。)
これは次のように頂点番号を振るとわかります。
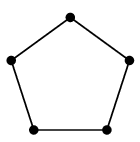 |
|
$\longrightarrow$ |
|
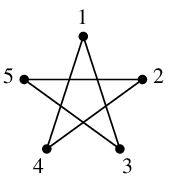 |
|
$\cong$ |
|
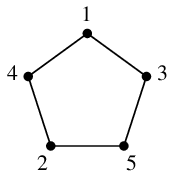 |
| $C_5$ |
| | |
$\overline{C_5}$ |
| | |
$C_5$ |
Prop.4 補グラフの補グラフ $\overline{\left(\overline{G}\right)}$ は $G$ と同型になる。
証明 隣接関係を2回逆転させるので元へ戻るから。(証明終)
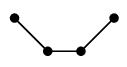
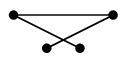
ここ大事! $\overline{P_n}$ や $\overline{K_{m,n}}$ を描くときは、頂点を一直線に並べない方が良い。
$P_4$ を真っ直ぐ描くと $\overline{P_4}$ の辺が描きにくいですが:
 |
|
$\longrightarrow$ |
|
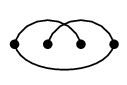 |
$P_4$ の頂点をずらして描いておけばこうなります:
 |
|
$\longrightarrow$ |
|
 |
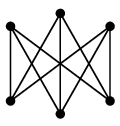
問 $\overline{K_{3,3}}$ を描いてみましょう。
答え
 |
|
$\longrightarrow$ |
|
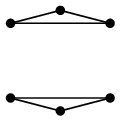 |
| $K_{3,3}$ |
| | |
$\overline{K_{3,3}}$ |
3. 連結性
Def.5 グラフが連結である、とは、2つの部分グラフの和にはなっていないこと。
和になっていると、全体としてはつながっていないよね、という意味です。


$C_3 \cup C_4$
Th.6 任意の有限無向グラフ $G$ は、連結な部分グラフたち ( $G$ の連結成分、と呼ぶ ) の和になる。
証明 $G$ が連結ならば $G$ の連結成分は $G$ ひとつ。$G$ が連結でなければ $G=G_1 \cup G_2$ と書け、
帰納法の仮定より $G_1$, $G_2$ は連結な部分グラフたちの和になるので。(証明終)
デモ動画
mp4 が再生可能なブラウザでご覧ください。各動画は 300~700KB です。
- 頂点の除去 ... 車輪グラフ $W_{10}$ から 3 頂点を除去
- 辺の縮約 ... 車輪グラフ $W_{10}$ の 1 辺を縮約
- 補グラフその1 ... 閉路グラフ $C_5$ の補グラフは $C_5$ 自身になる
- 補グラフその2 ... 完全二部グラフ $K_{3,4}$ の補グラフは $K_3 \cup K_4$
宿題
- ここから download
- 提出期限:こんなご時世ですので、急がなくていいです。
- 提出方法:スキャンするか写メを撮るかして、shiota@is.kochi-u.ac.jp 宛に送信してください(@は小文字)。
できなければ後日紙で提出しても構いません。
上手く送れない人はメールで連絡してください。
- 宿題を複数回分まとめて提出されると見落とす危険があります。
多少面倒でも1回分ずつ送信してください。
... 現在3科目担当していて合計130名程度の受講生がおります。
課題チェックの作業量をちょっと想像してみてください。
戻る



 →
→
 →
→