組合せとグラフの理論(塩田) 2020年度 第2回
今日のテーマ
- グラフの基本用語
- グラフの同型
- コンピュータ上でのグラフのデータ表現
絵の描き方の注意
印刷物やホームページではグラフの頂点を黒丸で描きますが、 黒板やノートで手書きのときは(塗りつぶす時間を節約するために)白丸で書きます。 → 手書きのときは
→ 手書きのときは
1. 無向グラフ
(1) グラフの表し方
もののつながり方に向きを考えないグラフを「無向グラフ」と呼びます。 無向グラフ $G$ は、その頂点集合 $V=V(G)$ と辺集合 $E=E(G)$ のペアとして表します: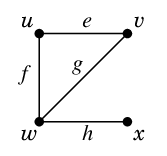
ただし、絵を見ずに $V=\{\,u,v,w,x\,\}$, $E=\{\,e,f,g,h\,\}$ だけ知っていても、 どの頂点が結ばれているのかはわかりません。そこで
(2) 辺の表し方の工夫
辺 $e$ が頂点 $u$ と $v$ を結ぶ辺であるとき、$e=uv$ と表すことにしましょう: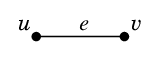
- $V=\{\,1,2,3\,\}$ なので、まず頂点 $1$, $2$, $3$ をプロットします。
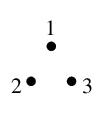
- $E$ の要素 $12$ と $23$ に従って、頂点 $1$ と $2$, $2$ と $3$ をそれぞれ辺で結びます。
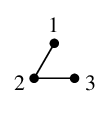
(3) ループ
ひとつの点から出てその点に戻る辺を「ループ」と呼びます。記号では $e=uu$ のように書ける辺のことです。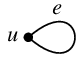
(4) 多重辺
ふたつの点の間に複数の辺があるとき、それらを「多重辺」と呼びます。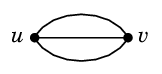
(5) 単純グラフ
ループも多重辺も持たないグラフを「単純グラフ」と呼びます。(6) 有限グラフ
頂点も辺も有限個であるグラフを「有限グラフ」と呼びます。(7) オーダー、サイズ
漢字は書くのに時間が掛かるので、英語を使って、- 頂点数(=頂点の個数)を「オーダー」
- 辺数(=辺の本数)を「サイズ」
2. 有向グラフ
もののつながり方に向きを考えたグラフを「有向グラフ」( digraph ) と呼びます。 有向グラフでは辺とは呼ばず「弧」( arc ) と呼び、 頂点 $u$ から出て $v$ へ至る弧を $a=uv$ と表します。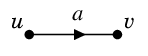
- $V=\{\,1,2,3\,\}$ なので、まず頂点 $1$, $2$, $3$ をプロットします。
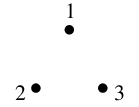
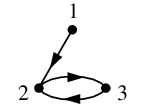
- $A$ の要素 $12$, $23$, $32$ に従って、頂点 $1$ から $2$ へ至る弧、
$2$ から $3$ へ至る弧、$3$ から $2$ へ至る弧をそれぞれ描きます。
3. その他の用語
(1) 隣接、接続
- 頂点と頂点が辺でつながっているとき、また、辺と辺がひとつの頂点を介してつながっているとき、それらは「隣接する」と言います。
- つながっている頂点と辺は「接続する」と言います。

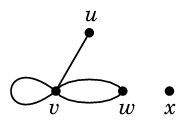
- $u$ の隣接点は $v$ と $w$
- $u$ と $x$ は隣接しない
- $e$ と $f$ は隣接する
- $e$ と $h$ は隣接しない
- $w$ の接続辺は $f$, $g$, $h$ の3本
※ ややこしいようですが、「隣」は同じもの同士に使う言葉、と覚えると良いでしょう。
(2) 点の次数
頂点 $u$ に接続する辺の本数を「 $u$ の次数」と呼び、$\rho(u)$ と表します。( $\rho$ はギリシャ文字のロー ) ループを 1 本で次数 2 と数える理由は- その1 $v$ の近くだけ切り取ると 5 本の辺が出ているように見えるから:
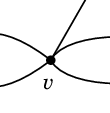
- その2 次の定理を成り立たせるため:
Ex.3 では、辺数は 4 で、次数の和は
(3) 部分グラフ
一部分でグラフになっているものを「部分グラフ」と呼びます。 例えば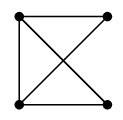
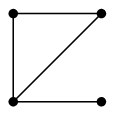 とか
とか
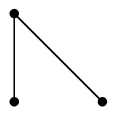 とか
とか
4. グラフの同型
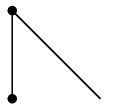
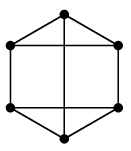
グラフはもののつながりを表す概念なので、「つながり方が同じである」ということを定義しましょう。 (1) による説明:$G$ の右下の頂点を左へ移動させ、下の 2 頂点を右へずらすと $H$ になります。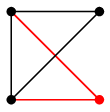 →
→
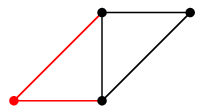 →
→
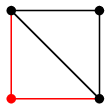
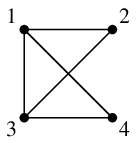
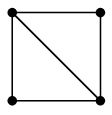
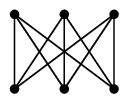
(2) による説明:次のように頂点の名前を付けると、どちらも辺集合が $\{\,12,13,14,23,34\,\}$ になります。
 ,
$H=$
,
$H=$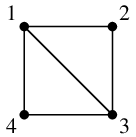
(3) による説明:次のように頂点の名前を付け、 $$\varphi(1)=u,\ \varphi(2)=v,\ \varphi(3)=w,\ \varphi(4)=x$$ と定めると、 隣接していない頂点は $G$ では $2$ と $4$, $H$ では $v=\varphi(2)$ と $x=\varphi(4)$ となって、 $\varphi$ によって隣接関係が写り合っています。
 ,
$H=$
,
$H=$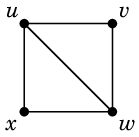
これは次のように頂点番号を振るとわかります(確かめてみましょう)。
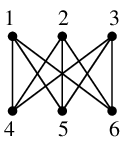 ,
$H=$
,
$H=$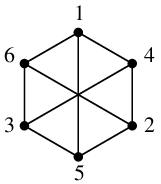
※ 例えば「一筆描きできるか否か」といった、つながり方に関する問題の答えは、同型なグラフであれば同じになります。ここ大事!
証明 動かせば同じ絵になるから。(証明終)
※ しかし、逆は言えません。ここ大事!
証明 $G$ は三角形を含むが $H$ は含まないから。(証明終)
5. コンピュータ上でのデータ表現
(1) 隣接行列 $A=\left( a_{ij} \right)$
頂点に $V=\{\,v_1,\cdots,v_n\,\}$ と番号を振って有向グラフでは
(2) 隣接リスト
$v_1$ の隣接点のリスト, $v_2$ の隣接点のリスト, $\cdots$, $v_n$ の隣接点のリスト を並べた二重リストを隣接リストと言います。例えば $v_2$ は $v_1$ との間に辺が 1 本、ループを 1 本、$v_3$ との間に二重辺を持ちますので、 隣接リストの 2 番目の子リストの要素は $v_1,v_2,v_3,v_3$ になります。
何故かというと、辺が少ないと隣接行列の要素はほとんど $0$ になるので、 検索に無駄な時間が掛かり、メモリもたくさん必要となるからです。
宿題
- ここから download ... 問題2(1)を訂正しました(4月24日)
- 提出期限:こんなご時世ですので、急がなくていいです。
- 提出方法:スキャンするか写メを撮るかして、shiota@is.kochi-u.ac.jp 宛に送信してください(@は小文字)。
できなければ後日紙で提出しても構いません。上手く送れない人はメールで連絡してください。 - 宿題を複数回分まとめて提出されると見落とす危険があります。 多少面倒でも1回分ずつ送信してください。 ... 現在3科目担当していて合計130名程度の受講生がおります。 課題チェックの作業量をちょっと想像してみてください。
 こういうのはダメ
こういうのはダメ
 ,
$H=$
,
$H=$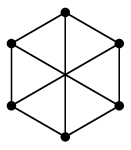
 ,
$H=$
,
$H=$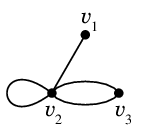 の隣接行列は
$A=\left(
\begin{array}{ccc}
0 & 1 & 0 \\
1 & 2 & 2 \\
0 & 2 & 0 \\
\end{array}
\right).
$
の隣接行列は
$A=\left(
\begin{array}{ccc}
0 & 1 & 0 \\
1 & 2 & 2 \\
0 & 2 & 0 \\
\end{array}
\right).
$
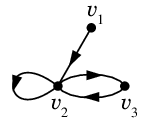 の隣接行列は
$A=\left(
\begin{array}{ccc}
0 & 1 & 0 \\
0 & 1 & 1 \\
0 & 1 & 0 \\
\end{array}
\right).
$
の隣接行列は
$A=\left(
\begin{array}{ccc}
0 & 1 & 0 \\
0 & 1 & 1 \\
0 & 1 & 0 \\
\end{array}
\right).
$