応用数学 第11回 (4) 熱伝導方程式再び
問題設定
前回扱った熱伝導方程式 を、今日は
境界条件を外して 解きます。
変数 $t$ はフーリエ変換の変数に使いますので、今日は時刻を $s$ で表します。
問 $u=u(x,s)$ についての熱伝導方程式
$\dps{c^2\frac{\partial^2 u}{\partial x^2}=\frac{\partial u}{\partial s}}$
を初期条件
$u(x,0)=f(x)$
のもとで解け。( ただし $f(x)$ は与えられた関数で、時刻 $s=0$ での熱分布を表す。)
境界条件をはずしたということは、棒が無限の長さを持っているということです。
Step 1 ( フーリエ変換 )
$u$ の、
$x$ についてのフーリエ変換を $\hat u$ と表すと、
Th.4 (2) より
$\dps{\widehat{\left(\frac{\partial^2 u}{\partial x^2}\right)}=(it)^2\hat u=-t^2\hat u}$
\begin{align}
\therefore
\frac{\partial \hat u}{\partial s}
& = \frac{\partial}{\partial s} \left( \frac{1}{\sqrt{2\pi}} \int_{-\infty}^{\infty} u(x,s) e^{-itx}dx \right) \\
& = \frac{1}{\sqrt{2\pi}} \int_{-\infty}^{\infty} \left(\frac{\partial}{\partial s} u(x,s)\right) e^{-itx}dx \\
& = \frac{1}{\sqrt{2\pi}} \int_{-\infty}^{\infty} \left(c^2\frac{\partial^2 u}{\partial x^2}\right) e^{-itx}dx \\
&= c^2 \widehat{\left(\frac{\partial^2 u}{\partial x^2}\right)} = -c^2t^2\hat u \\
\end{align}
$s$ の関数として解くと
$\dps{\hat u = Ce^{-c^2t^2s}}$
初期条件より
$\dps{\hat u(t,0)=\widehat{u(x,0)}=\hat f(t)}$
ゆえ
$\dps{C= Ce^{-c^2t^2\times 0}=\hat u(t,0)=\hat f(t)}$
よって
$\dps{\hat u(t, s)=\hat f(t)e^{-c^2st^2}}$
Step 2 ( フーリエ逆変換 )
この式をフーリエ逆変換すると、
Th.7 より
$\dps{u(x,s)=\frac{1}{\sqrt{2\pi}}f(x) * ( e^{-c^2st^2}}$ のフーリエ逆変換 $)$
Ex.8 を使うために $\dps{\frac{1}{4\alpha}=c^2s}$ とおくと $\dps{\alpha=\frac{1}{4c^2s}}$ で
$\dps{( e^{-c^2st^2}}$ のフーリエ逆変換
$\dps{)=\sqrt{2\alpha}e^{-\alpha x^2}=\frac{1}{c\sqrt{2s}}e^{-x^2/(4c^2s)}}$
よって
$\dps{u(x,s)=\frac{1}{2c\sqrt{\pi s}} \int_{-\infty}^{\infty} f(x-y)\, e^{-y^2/(4c^2s)}dy}$.
積分表示の形で解が得られました。
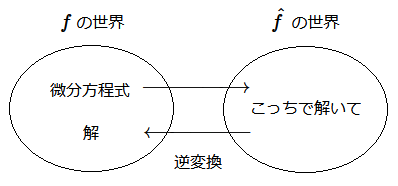
次回から勉強するラプラス変換は、
この「変換して、簡単に解いて、逆変換」というパターンで微分方程式を解くための
強力な道具です。
