応用数学 10回 (3) 波動方程式の解法
波動方程式
Def.7 次の形の偏微分方程式を「波動方程式」と呼ぶ:
$$c^2\frac{\partial^2 u}{\partial x^2}=\frac{\partial^2 u}{\partial t^2}
\tag{6.1}
$$
これは、$x$ 軸上の区間 $0 \leqq x \leqq \ell$ に張られた
弦の変位 $u(x,t)$ が満たす方程式です。
問 $(6.1)$ を、
- 境界条件 $u(0,t)=u(\ell,t)=0$
- 初期条件 $u(x,0)=f(x)$, $\dps{\frac{\partial u}{\partial t}(x,0)=g(x)}$
のもとで解け ( ただし $f(x)$, $g(x)$ は与えられた関数 ) 。
境界条件は、弦の両端が $x$ 軸に固定されていることを、
初期条件の $f(x)$, $g(x)$ は時刻 $t=0$ での弦の変位と速度を表します。
Step 1 ( 変数分離解 )
前ページと同様
$u(x,t)=X(x)T(t)$ ( $X(x)$ は $x$ だけの、$T(t)$ は $t$ だけの関数 )
の形の「変数分離解」を探します。今度は
$\dps{\frac{X''}{X}=\frac{1}{c^2}\frac{T''}{T}}=$ 定数 $(-k)$
となります。境界条件 $X(0)=X(\ell)=0$ から
L'a 2 を用いて
$\exists\, n$; $\dps{k=\left(\frac{n\pi}{\ell}\right)^2}$
かつ $\dps{X=A\sin\left(\frac{n\pi x}{\ell}\right)}$
となるところは一緒で、$T$ は
$\dps{T=B\cos\left(\frac{n\pi c t}{\ell}\right)+B'\sin\left(\frac{n\pi c t}{\ell}\right)}$
となります。掛け合わせて
$\dps{U = XT = \sin\left(\frac{n\pi x}{\ell}\right)
\left\{C\cos\left(\frac{n\pi c t}{\ell}\right)+D\sin\left(\frac{n\pi c t}{\ell}\right)\right\}
}$
となります。
Step 2 ( 重ね合わせの原理 )
今度も、変数分離解を重ね合わせた
$\dps{u(x,t)=\sum_{n=1}^{\infty} \sin\left(\frac{n\pi x}{\ell}\right)
\left\{C_n\cos\left(\frac{n\pi c t}{\ell}\right)+D_n\sin\left(\frac{n\pi c t}{\ell}\right)\right\}}$
が初期条件を満たすように $C_n$, $D_n$ を決めます。
$t=0$ を入れると
$\dps{f(x)=u(x,0)=\sum_{n=1}^{\infty} C_n \sin\left(\frac{n\pi x}{\ell}\right) }$.
また
$\dps{\frac{\partial u}{\partial t}(x,t)
=\sum_{n=1}^{\infty} \sin\left(\frac{n\pi x}{\ell}\right)
\left(\frac{n\pi c}{\ell}\right)\left\{-C_n\sin\left(\frac{n\pi c t}{\ell}\right)
+D_n\cos\left(\frac{n\pi c t}{\ell}\right)\right\}}$
に $t=0$ を入れて
$\dps{g(x)=\frac{\partial u}{\partial t}(x,0)
=\sum_{n=1}^{\infty} \left(\frac{n\pi c}{\ell}\right)D_n\sin\left(\frac{n\pi x}{\ell}\right) }$.
$f(x)$、$g(x)$ のフーリエ正弦展開から
$\dps{C_n = \frac{2}{\ell}\int_{0}^{\ell}f(x)\sin\left(\frac{n\pi x}{\ell}\right)dx,}$
$\quad
\dps{D_n = \frac{2}{n\pi c}\int_{0}^{\ell}g(x)\sin\left(\frac{n\pi x}{\ell}\right)dx.}$
例
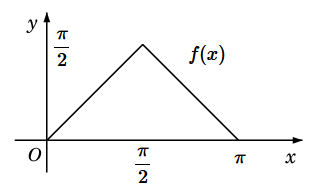
Ex.8 $\ell=\pi$,
$\dps{
f(x)=
\left\{
\begin{array}{ll}
x & (\ 0 \leqq x \leqq \displaystyle{\frac{\pi}{2}} \ ) \\
\pi-x & (\ \displaystyle{\frac{\pi}{2}} \leqq x \leqq \pi \ ) \\
\end{array}
\right.,
}$
$g(x)=0$ のとき
教科書 pp.101-102, 例 3.2 より
$\dps{f(x)=\frac{4}{\pi}\left(\sin(x)-\frac{\sin(3x)}{3^2}+\frac{\sin(5x)}{5^2}-\cdots\right)}$
ですから、
$\dps{u(x,t)=\frac{4}{\pi}\left(\sin(x)\cos(ct)
-\frac{\sin(3x)}{3^2}\cos(3ct)
+\frac{\sin(5x)}{5^2}\cos(5ct)-\cdots\right)}$
横軸を $x$, 縦軸を振幅としてシミュレーションしてみると
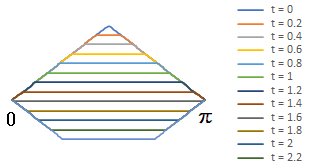
となります。
三角形の形に弦を引っ張って離すと、台形の形になって低くなってゆき、反対側にまた台形の形で膨らんでゆくことがわかります。
ストークスの波動公式
Th.9 ( ストークスの波動公式 ) 「$(6.1)+$ 境界条件 $+$ 初期条件」の解は次のようにも書ける:
$\dps{
u(x,t)=\frac{1}{2}\Big\{f(x-ct)+f(x+ct)\Big\}
+\frac{1}{2c}\int_{x-ct}^{x+ct}g(x)dx
}$
証明は教科書 pp.114-115 を見てください。
Ex.8 では
$\dps{
u(x,t)=\frac{1}{2}\Big\{f(x-ct)+f(x+ct)\Big\}
}$
となり、時刻 $t$ での波形は、初期の三角形の波形を左右に $ct$ だけシフトした波形の平均で台形になります。
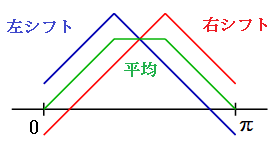
上のシミュレーションの通りです。


