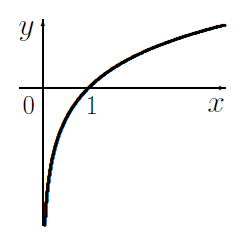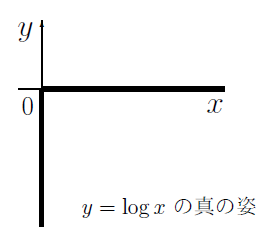アルゴリズム論特論(塩田)第1回 (2) ビット長
ビット長
Def.1 正整数(= 自然数)$n$ の、2進数としての桁数を $n$ のビット長(またはビット数)と言う。
次は全て同じことの言い換えです:
- $n$ のビット長は $k$ である
- $n$ は $k$-ビットの数である
- $n$ は $k$ 桁の2進数として表される
Th.2 自然数 $n$ のビット長を $k$ とすると $k = \lfloor \log_2 n\rfloor + 1$.
( ただし $\lfloor\ \rfloor$ は切り捨ての記号 )
証明 $k$-ビットで最小の自然数は $(100\cdots 00)_2 = 2^{k-1}$ であり、$k$-ビットで最大の自然数は $(111\cdots 11)_2 = 2^k-1$ です。従って
$$2^{k-1} \leqq n \leqq 2^k - 1 \lt 2^k.$$
$$\mbox{∴}\quad k-1 \leqq \log_2 n \lt k.$$
つまり $\log_2 n$ は $k-1$ 以上 $k$ 未満の実数であるので $\lfloor \log_2 n \rfloor = k - 1.$ (証明終)
$O$ 記法
Def.3 2つの関数 $f(n)$, $g(n)$ が
$$\lim_{n\rightarrow \infty} \left|\frac{f(n)}{g(n)}\right| \leqq \mbox{定数}$$
を満たすとき $f(n) = O(g(n))$ と表す。
- これは関数の大きさを大雑把に表す記号です。( 大雑把の $O$、といったところです。)
- アルゴリズムの計算量を入力引数のビット長で表すために使います。
Ex.4
- $100\,n^2 = O(n^2)$ : 定数倍は無視します。
... 入力サイズが2倍になったら計算時間が何倍になるか、といようなうことが知りたくて計算量を測るのですが、そのことには定数倍は必要ないからです。
また、マシンスペック(例えばクロック周波数)が違えば同じアルゴリズムでも計算時間は一定の倍数違ってきますので、そこは気にしない、と考えてもよいでしょう。
- $n^3+100\,n^2=O(n^3)$ : 多項式関数はべき指数の大きい方が強いので、一番べき指数の大きい項に吸収されます。
- $2^n + x^{100} = O(2^n)$ : 指数関数はどんな多項式関数より強力です。逆に言うと、計算量が指数関数であるようなアルゴリズムは使い物にならない、ということです。
Th.5 自然数 $n$ のビット長 $= O(\log n)$
$\log x$ の真の姿
問 関数 $y=\log x$ のグラフは描けますか?
閉じる
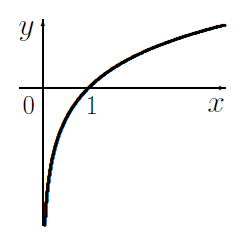
(理系の大学院生がこんなん間違ったらあきませんよ。)
しかし、暗号屋にとってはこういうイメージです:
例えば RSA暗号では 2048ビット程度の整数を扱います。$x=2^{2048}$ 位になると
$$\log x = 2048 \times \log 2 \mbox{ ≒ } 1419.565 \lt 2^{11}$$
ですから
$$\frac{\log x }{x} \lt 2^{11-2048} \lt 2^{-2000} = 1024^{-200} \lt 10^{-600}$$
小数点以下 0 が600個以上続くぐらいグラフは $x$軸にへばりついているわけです。
計算量にとって $n$ と $\log n$ は天と地の差があって、例えば
- バブルソートの計算量は $O(n^2)$
- マージソートの計算量は $O(n \log n)$
ですから、入力サイズが大きくなればマージソートは遥かにバブルソートより強力、ということになります。