アルゴリズム論特論(塩田)第13回 (3) 3 式以上の中国剰余アルゴリズム
前へ / 戻る / 次へ
$\newcommand{\ol}[1]{\overline{#1}}$
$\newcommand{\znz}[1]{\mathbb{Z}/#1 \mathbb{Z}}$
$\newcommand{\znzc}[1]{(\mathbb{Z}/#1 \mathbb{Z})^{\times}}$
$\newcommand{\inv}[1]{\displaystyle{\frac{1}{#1}}}$
式が 3 個以上のときの中国剰余アルゴリズム
Th.5(中国剰余定理) $m_1$, $\cdots$ $m_k$ を互いに素な $k$ 個の法とするとき、連立合同式
$\dps{
\left\{
\begin{array}{c}
x \equiv a_1 \pmod{m_1} \\
\vdots \\
x \equiv a_k \pmod{m_k} \\
\end{array}
\right.}$
は $\bmod (m_1\times \cdots \times m_k)$ で唯一の解 $x$ を持つ。
証明 唯一性は
Th.1 と同様に示せます。
解は次の
Alg.6 や
Alg.8 で構成できます。
Algorithm 6(中国剰余アルゴリズム) Th.5 の状況で
- 入力:$a_1$, $\cdots$ $a_k$; $m_1$, $\cdots$ $m_k$
- 出力:$x$
$A=a_1$, $M=m_1$
for $i=2$
to $n$ :
新$A =$ 連立合同式 $\dps{
\left\{
\begin{array}{c}
x \equiv A \pmod{M} \\
x \equiv a_i \pmod{m_i} \\
\end{array}
\right.}$ の解
... Alg.2 を用いて求める
新$M = M \times m_i$
$A$ を出力
証明 ループ変数が $i$ のときの 新$A$ は、連立合同式
$\dps{
\left\{
\begin{array}{c}
x \equiv a_1 \pmod{m_1} \\
\vdots \\
x \equiv a_i \pmod{m_i} \\
\end{array}
\right.}$
の解になっていて、この $i$ 個の合同式と
$x \equiv $ 新$A\ ( \bmod$ 新$M)$
が同値になっています。(証明終)
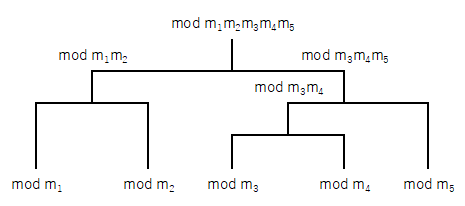
※ 図のようなトーナメントで合同式を制覇してゆくイメージです。
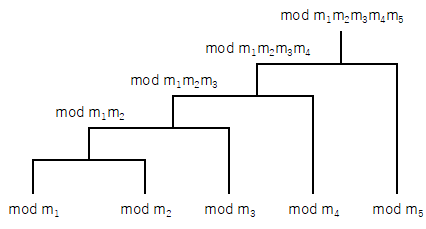
トーナメントはどんな組み方をしても答えは同じになります。
Ex.7 Alg.5 に従って連立合同式
$\dps{
\left\{
\begin{array}{cl}
(1) & x \equiv \ 3\ \pmod{\ 7\ } \\
(2) & x \equiv \ 5\ \pmod{17} \\
(3) & x \equiv 11 \pmod{37} \\
\end{array}
\right.}$
を解いてみましょう。Ex.3 から
(1) かつ (2) $\Leftrightarrow$ $x \equiv 73 \pmod{119}$
でした。ですから
$\dps{
\left\{
\begin{array}{l}
x \equiv 73 \pmod{119} \\
x \equiv 11 \pmod{\ 37\ } \\
\end{array}
\right.}$
を解けばよく
$119 \times 14 + 37 \times (-45) = 1$
から
$x=(73 \times 37 \times (-45) + 11 \times 119 \times 14 ) \,\%\, 4403 = 2453$
もうひとつのアルゴリズム
次のアルゴリズムは $k$ 個まとめて解くやり方です。
Algorithm 8(中国剰余アルゴリズム) Th.5 の状況で
- 入力:$a_1$, $\cdots$ $a_k$; $m_1$, $\cdots$ $m_k$
- 出力:$x$
- $M=m_1\times \cdots \times m_k$ とおく。
- 各 $i=1,\cdots,k$ に対し、$M_i=M/m_i$ とおく。
- 各 $i=1,\cdots,k$ に対し、$m_i$, $M_i$ を引数として拡張ユークリッドアルゴリズムを実行し
$m_iu_i+M_iv_i=1$
を満たす $u_i$, $v_i$ を求める。
- $\dps{x = \sum_{i=1}^k a_i(M_iv_i) \,\%\, M}$ とおく。
証明 $M_i$ は $m_i$ 以外の法の積なので、
Alg.2 の証明と同様に
| $M_1v_1$ | $M_2v_2$ | $\cdots$ | $M_kv_k$ |
| $\bmod m_1$ | $1$ | $0$ | $\cdots$ | $0$ |
| $\bmod m_2$ | $0$ | $1$ | $\cdots$ | $0$ |
| $\vdots$ | $\vdots$ | $\vdots$ | $\ddots$ | $\vdots$ |
| $\bmod m_k$ | $0$ | $0$ | $\cdots$ | $1$ |
が成り立ちます。従って mod $m_j$ では
$\dps{x \equiv \sum_{i=1}^k a_i(M_iv_i) \equiv a_j(M_jv_j) + \sum_{i \neq j} a_i(M_iv_i)
\equiv a_j\times 1 + \sum_{i \neq j} a_i\times 0 = a_j}$
(証明終)
Ex.9 $m_1=3$, $m_2=5$, $m_3=7$ のとき、
- $M=3\times 5 \times 7=105$
- $M_1=5 \times 7 =35$, $M_2=3 \times 7=21$, $M_3=3 \times 5 =15$
- $3 \times(-23) + 35 \times 2=1$, $5 \times (-4) + 21 \times 1 = 1$, $7 \times (-2) + 15 \times 1 = 1$
- $x = (70 \times a_1 + 21 \times a_2 + 15 \times a_3) \,\%\, 105$
これを使ったのが今日の最初の数当てゲームです。
数字が簡単なので昔から手品に使われていたらしく、
3~5世紀ごろの作と言われる中国の数学書「孫子算経」に書かれていることから中国剰余定理と呼ばれています。
計算量
Th.10 Alg.6,Alg.8 の計算量は $O(k\log^2 M)$ である。
特に $k$ が 小さく固定されている場合は $O(\log^2 M)$ になる。

