アルゴリズム論特論(塩田)第11回 (3) $\bmod\ p$ の乗法構造
前へ / 戻る / 次へ
$\newcommand{\ol}[1]{\overline{#1}}$
$\newcommand{\znz}[1]{\mathbb{Z}/#1 \mathbb{Z}}$
$\newcommand{\znzc}[1]{(\mathbb{Z}/#1 \mathbb{Z})^{\times}}$
$\newcommand{\inv}[1]{\displaystyle{\frac{1}{#1}}}$
"観察結果" の証明
前々ページの観察結果を定理として書いておきましょう。
Th.4 $a \in \znzc{p}$ の位数を $e$ とするとき、次が成り立つ。
- $e$ は $p-1$ の約数である。
- $a^1$, $\cdots$, $a^{p-1}$ は、$a^e$ から先は繰り返しになる。
- (2) の繰り返しの周期は $a$ の位数 $e$ に等しい。
- $a^1$, $\cdots$, $a^{p-1}$ には同じ数が $(p-1)/e$ 回ずつ現れる。
証明 (1) フェルマの小定理より $a^{p-1} = 1$ ですから
Th.3 より。
(2)-(4) これは
$a^{e+1} = a^e \times a^1 = a^1$,
$a^{e+2} = a^e \times a^2 = a^2$,
$\vdots$
より必然的にそうなります。(証明終)
生成元
観察 (5) も証明されていて
Th.5 任意の素数 $p$ に対して、
$g^1$, $\cdots$, $g^{p-1}$ がすべて異なるような $g \in \znzc{p}$ が必ず存在する。
このような $g$ にも名前がついています。
Def.6 Th.3 の $g$ を $\bmod\ p$ の生成元 ( generator )、あるいは原始根 ( primitive root ) と呼ぶ。
$g$ と書いたのは generator の頭文字だからですが、
何故 generator と呼ぶかという理由は次の (3) です。
Th.7 次は同値である。
- $g$ は $\bmod\ p$ の生成元である。
- $g^1$, $\cdots$, $g^{p-1}$ はすべて異なる
- $g^1$, $\cdots$, $g^{p-1}$ は全体として $1$, $2$, $\cdots$, $p-1$ に等しい。
- $g$ の位数は $p-1$ である。
この状態を群論用語では、「$\znzc{p}$ は $g$ によって生成される巡回群である」と言う。
$g$ のべき乗が mod $p$ のすべての既約剰余類を
生成する、と言う意味です。
絵としては $g$ のべき乗たちは巡回的に並んでいるので「巡回群」と呼びます。
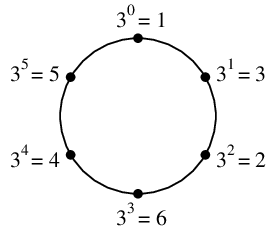
$p=7$, $g=3$ の例では次の図のようになって、
$3^6=1=3^0$ から2周目に突入する、という感じです。
 Th.7 の証明
Th.7 の証明 $\znzc{p}$ の要素は丁度 $p-1$ 個あるので (3) が言え、(4) は
Th.2 (4) より従います。(証明終)
Th.5 の証明は初等的にできますが、そんなに短くはないので省略します。
(初等整数論あるいは公開鍵暗号の教科書には大抵書いてあります。)
